
科目: 来源: 题型:填空题
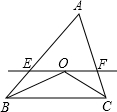 如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的平分线,过点O作EF∥BC,分别与边AB、AC相交于点E、F,AB=8,AC=7,那么△AEF的周长等于15.
如图,在△ABC中,OB、OC分别是∠ABC和∠ACB的平分线,过点O作EF∥BC,分别与边AB、AC相交于点E、F,AB=8,AC=7,那么△AEF的周长等于15.查看答案和解析>>
科目: 来源: 题型:解答题
 自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:| 选项 | 频数 | 频率 |
| A | 30 | M |
| B | n | 0.2 |
| C | 5 | 0.1 |
| D | 5 | 0.1 |
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | 对角线互相垂直且相等的平行四边形是正方形 | |
| B. | 对角线互相垂直的矩形是正方形 | |
| C. | 对角线相等的菱形是正方形 | |
| D. | 对角线互相垂直的四边形是正方形 |
查看答案和解析>>
科目: 来源: 题型:解答题
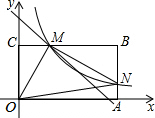 如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.
如图,矩形OABC,点A,C分别在x轴,y轴正半轴上,直线y=-x+6交边BC于点M(m,n)(m<n),并把矩形OABC分成面积相等的两部分,过点M的双曲线y=$\frac{k}{x}$(x>0)交边AB于点N.若△OAN的面积是4,求△OMN的面积.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
 如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.
如图,在四边形ABCD中,AB=AD,对角线AC,BD交于点E,点O在线段AE上,⊙O过B,D两点,若OC=5,OB=3,且cos∠BOE=$\frac{3}{5}$.求证:CB是⊙O的切线.查看答案和解析>>
科目: 来源: 题型:填空题
查看答案和解析>>
科目: 来源: 题型:填空题
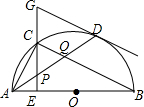 如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是$\widehat{AD}$的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中正确结论是②③(只需填写序号).
如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是$\widehat{AD}$的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中正确结论是②③(只需填写序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com