12．在?ABCD中，若∠A+∠C=160°，则∠C的度数为80°．

11．（1）如图①，AD是△ABC的中线，△ABD与△ACD的面积有怎样的数量关系？为什么？
（2）若三角形的面积记为S，例如：△ABC的面积记为S_△ABC，如图②，已知S_△ABC=1，△ABC的中线AD、CE相交于点O，求四边形BDOE的面积．
小华利用（1）的结论，解决了上述问题，解法如下：
连接BO，设S_△BEO=x，S_△BDO=y，
由（1）结论可得：S${\;}_{△BCE}={S}_{ABD}=\frac{1}{2}{S}_{△ABC}=\frac{1}{2}$，
                S_△BCO=2S_△BDO=2y，
                S_△BAO=2S_△BEO=2x．
则有$\left\{\begin{array}{l}{{S}_{△BEO}+{S}_{△BCO}={S}_{△BCE}}\\{{S}_{△BAO}+{S}_{△BDO}={S}_{△BAD}}\end{array}\right.$，即$\left\{\begin{array}{l}{x+2y=\frac{1}{2}}\\{2x+y=\frac{1}{2}}\end{array}\right.$．
所以$x+y=\frac{1}{3}．即四边形BDOE面积为\frac{1}{3}$．
请仿照上面的方法，解决下列问题：
①如图③，已知S_△ABC=1，D、E是BC边上的三等分点，F、G是AB边上的三等分点，AD、CF交于点O，求四边形BDOF的面积．
②如图④，已知S_△ABC=1，D、E、F是BC边上的四等分点，G、H、I是AB边上的四等分点，AD、CG交于点O，则四边形BDOG的面积为$\frac{1}{10}$．

10．计算：-2²$+（π-2015）^{0}+（\frac{1}{2}）^{-2}$．

9．现有长为57cm的铁丝，要截成n（n＞2）小段，每小段的长度为不小于1cm的整数，如果其中任意3小段都不能拼成三角形，则n的最大值为8．

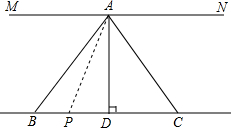8．已知：如图，AD平分∠BAC，且AD⊥BC于点D，MN∥BC，请在括号中补全步骤的推理理由．
（1）试说明∠BAM=∠CAN．
∵MN∥BC，（　　）
∴∠BAM=∠ABC，∠CAN=∠ACB．（　　）
又∵AD⊥BC，（　　）
∴∠ADB=∠ADC=90°，（　　）
∴∠BAD+∠ABC=90°，∠CAD+∠ACB=90°，
又∵AD平分∠BAC，（　　）
∴∠BAD=∠CAD，（　　）
∴∠ABC=∠ACB，（　　）
∴∠BAM=∠CAN，（　　）
（2）如果AD=5cm，点P是直线BC上的一个动点，连接AP，则AP不小于5cm．
∵AD⊥BC，AD=5cm，
∴AP≥5cm．（　　）

7．如图：在平面直角坐标系中有△ABC，将△ABC向x轴的负方向平移4个单位得到△A₁B₁C₁，使A点的对应点为A₁，B、C的对应点分别为B₁、C₁．
（1）画出△A₁B₁C₁；线段A₁A和线段B₁B有什么数量关系和位置关系．
（2）分别写出A₁、B₁、C₁的坐标．
（3）求△ABC的面积．

6．2016年8月5日，第31届奥运会将在巴西里约热内卢举行，某中学开展了“你最喜欢收看的奥运五项球赛（只选一项）”抽样调查，根据调查数据，小浩计算出喜欢收看篮球比赛的人数占抽样人数的19%等相关数据，小颖则绘制了如下不完整的统计图：

请根据两位同学提供的信息，解答下面的问题：
（1）共抽查了多少名学生？
（2）将条形统计图补充完整；
（3）在扇形统计图中，“羽毛球”部分所对应的圆心角是多少度？
（4）根据以上调查，试估计该校2500名学生中，最喜欢收看乒乓球比赛的人数．

5．计算：|1-$\sqrt{2}$|+|$\sqrt{3}-1$|-|$\sqrt{2}-\sqrt{3}$|．

4．如图，直线AB，CD相交于点O，OA平分∠EOC，若∠EOC：∠EOD=2：3，∠BOD=36度．

3．把方程3x+2y-1=0改写成用含x的式子表示y的形式是y=$\frac{1-3x}{2}$．