7．证明：2²⁰¹²+2²⁰¹¹-2²⁰¹⁰能被5整除．

6．设a，b都是有理数，规定：a*b=a²+b²，试求4*8*[2*（-3）]的值．

5．用适当的方法解方程：（2x-3）²=9（2x+3）²．

4．定义一种对正整数n的“F运算”：①当n为奇数时，结果为3n+5；②当n为偶数时，结果为$\frac{n}{{2}^{k}}$（其中k是使$\frac{n}{{2}^{k}}$为奇数的正整数），并且运算重复进行．例如，取n=18时，则：

若n=31，则第31次“F运算”的结果是1．

3．已知0＜x＜1，且x+$\frac{1}{x}$=$\sqrt{8}$，求x-$\frac{1}{x}$的值．

2．无论x取何值时，等式ax+b-4x=3恒成立，求a，b的值．

1．下列等式：
$\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$
将以上三个等式两边分别相加得
$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$
（1）猜想：$\frac{1}{n（n+1）}$=$\frac{1}{n}$-$\frac{1}{n+1}$；
（2）直接写出下列各式的结果
①$\frac{1}{1×2}$+$\frac{1}{2×3}$+…+$\frac{1}{2013×2014}$=$\frac{2013}{2014}$；
②$\frac{1}{100×101}$+$\frac{1}{101×102}$+…+$\frac{1}{n（n+1）}$=$\frac{n-99}{100（n+1）}$．
（3）探究并计算：$\frac{1}{2×4}$+$\frac{1}{4×6}$+$\frac{1}{6×8}$+…+$\frac{1}{2012×2014}$．

20．根据指令[s，A]（s≥0，0°＜A＜180°），机器人在平面上能完成下列动作：先原地逆时针旋转角度A，再朝其面对的方向沿直线行走距离s，现机器人在直角坐标系的坐标原点，且面对x轴正方向．
（1）若给机器人下了一个指令[4，180°]，则机器人应移动到点（-4，0）；
（2）请你给机器人下一个指令[5，90°]，使其移动到点（0，5）．

19．将抛物线y=x²-4x+3向上平移至顶点落在x轴上，如图所示，将两条抛物线、对称轴和y轴围成的图形的面积S（图中的阴影部分）是2．

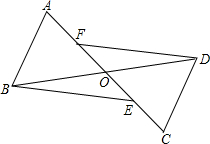18．如图，线段AC与BD相交于点O，连接AB，CD，若AB∥CD，BO=DO，AF=CE．
（1）请说明点O是AC的中点；
（2）猜想BE与DF的数量关系和位置关系，并说明理由．