2．一元一次方程4x+1=0的解是（　　）

A．

$\frac{1}{4}$

B．

-$\frac{1}{4}$

C．

4

D．

-4

1．据《梧州日报》报道，梧州黄埔化工药业有限公司位于万秀区松脂产业园，总投资119000000元，数字119000000用科学记数法表示为（　　）

A．

119×106

B．

11.9×107

C．

1.19×108

D．

0.119×109

20．在下列图形中，是轴对称图形的是（　　）

A．

B．

C．

D．

19．|-$\frac{1}{5}$|=（　　）

A．

-$\frac{1}{5}$

B．

$\frac{1}{5}$

C．

5

D．

-5

18．观察下列运算：8¹=8，8²=64，8³=512，8⁴=4096，8⁵=32768，8⁶=262144，…则8¹+8²+8³+8⁴…+8²⁰¹⁵的和的个位数字是4．

17．如图，二次函数y=ax²+bx+c（a≠0）的图象经过点（0，3），且当x=1时，y有最小值2．
（1）求a，b，c的值；
（2）设二次函数y=k（2x+2）-（ax²+bx+c）（k为实数），它的图象的顶点为D．
①当k=1时，求二次函数y=k（2x+2）-（ax²+bx+c）的图象与x轴的交点坐标；
②请在二次函数y=ax²+bx+c与y=k（2x+2）-（ax²+bx+c）的图象上各找出一个点M，N，不论k取何值，这两个点始终关于x轴对称，直接写出点M，N的坐标（点M在点N的上方）；
③过点M的一次函数y=-$\frac{3}{4}$x+t的图象与二次函数y=ax²+bx+c的图象交于另一点P，当k为何值时，点D在∠NMP的平分线上？
④当k取-2，-1，0，1，2时，通过计算，得到对应的抛物线y=k（2x+2）-（ax²+bx+c）的顶点分别为（-1，-6，），（0，-5），（1，-2），（2，3），（3，10），请问：顶点的横、纵坐标是变量吗？纵坐标是如何随横坐标的变化而变化的？

16．某兴趣小组开展课外活动．如图，A，B两地相距12米，小明从点A出发沿AB方向匀速前进，2秒后到达点D，此时他（CD）在某一灯光下的影长为AD，继续按原速行走2秒到达点F，此时他在同一灯光下的影子仍落在其身后，并测得这个影长为1.2米，然后他将速度提高到原来的1.5倍，再行走2秒到达点H，此时他（GH）在同一灯光下的影长为BH（点C，E，G在一条直线上）．
（1）请在图中画出光源O点的位置，并画出他位于点F时在这个灯光下的影长FM（不写画法）；
（2）求小明原来的速度．

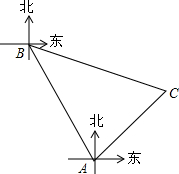15．某海域有A，B两个港口，B港口在A港口北偏西30°方向上，距A港口60海里，有一艘船从A港口出发，沿东北方向行驶一段距离后，到达位于B港口南偏东75°方向的C处，求该船与B港口之间的距离即CB的长（结果保留根号）．

14．图①是我们常见的地砖上的图案，其中包含了一种特殊的平面图形-正八边形．

（1）如图②，AE是⊙O的直径，用直尺和圆规作⊙O的内接正八边形ABCDEFGH（不写作法，保留作图痕迹）；
（2）在（1）的前提下，连接OD，已知OA=5，若扇形OAD（∠AOD＜180°）是一个圆锥的侧面，则这个圆锥底面圆的半径等于$\frac{15}{8}$．

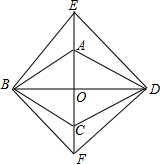13．如图，菱形ABCD的对角线AC，BD相交于点O，分别延长OA，OC到点E，F，使AE=CF，依次连接B，F，D，E各点．
（1）求证：△BAE≌△BCF；
（2）若∠ABC=50°，则当∠EBA=20°时，四边形BFDE是正方形．