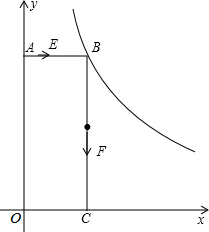19．如图，已知：矩形AOCB的顶点B在反比例函数y=$\frac{k}{x}$（k＞0，x＞0）的图象上，且AB=3，BC=8．
（1）求反比例函数的关系式；
（2）若动点E从A开始沿AB向B以每秒1个单位长度的速度运动，同时动点F从B开始沿BC向C以每秒2个单位长度的速度运动，当其中一个动点到达端点时，另一个动点随之停止运动，设运动时间为t秒，
①当t为何值时，△BEF是等腰直角三角形？
②当t=2时，在双曲线上是否存在一点M，使得四边形EFBM为平行四边形？说明理由；
（3）若在（2）中的条件下，运动1秒时，在y轴上是否存在点D，使△DEF的周长最小？若存在，请求出△DEF的周长最小值；若不存在，请说明理由．

18．如图，将△ABC绕点A逆时针旋转40°到△AB′C′的位置，则∠ACC′=70°．

17．如图，在A时测得旗杆的影长是4米，B时测得的影长是9米，两次的日照光线恰好垂直，则旗杆的高度是6米．

16．如果一个四边形的两条对角线互相平分，互相垂直且相等，那么这个四边形是正方形．

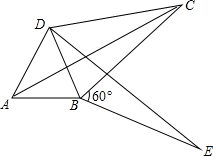15．给出定义：若一个四边形中存在相邻两边的平方和等于一条对角线的平方，则称该四边形为勾股四边形．
（1）在你学过的特殊四边形中，写出两个勾股四边形的名称；
（2）如图，将△ABC绕顶点B按顺时针方向旋转60°后得到△DBE，连接
AD、DC，若∠DCB=30°，求证：四边形ABCD是勾股四边形．

14．直线l₁∥l₂∥l₃，正方形ABCD的三个顶点A、B、C分别在l₁、l₂，l₃上，l₁、l₂之间的距离是4，l₂，l₃之间的距离是5，则正方形ABCD的面积是41．

13．如图，过原点的抛物线y=-$\frac{1}{2}$x²+bx+c与x轴交于点A（4，0），B为抛物线的顶点，连接OB，点P是线段OA上的一个动点，过点P作PC⊥OB，垂足为点C．
（1）求抛物线的解析式，并确定顶点B的坐标；
（2）设点P的横坐标为m，将△POC绕着点P按顺利针方向旋转90°，得△PO′C′，当点O′和点C′分别落在抛物线上时，求相应的m的值；
（3）当（2）中的点C′落在抛物线上时，将抛物线向左或向右平移n（0＜n＜2）个单位，点B、C′平移后对应的点分别记为B′、C″，是否存在n，使得四边形OB′C″A的周长最短？若存在，请直接写出n的值和抛物线平移的方向，若不存在，请说明理由．

12．如图1，AD是△ABC的中线，过点D的直线交AB边于点M，交AC边的延长线于点N．
①若AM=$\frac{3}{4}$AB，求$\frac{NC}{NA}$的值．
分析：在图1中，作CF∥AB交MN于点F，则BM与CF的数量关系是相等，由AM=$\frac{3}{4}$AB，可得BM与AM的数量关系是BM=$\frac{1}{3}$AM，所以$\frac{NC}{NA}$的值是$\frac{1}{3}$．
②若AM=mAB（m＞0），求$\frac{NC}{NA}$的值（用含m的代数式表示）
（2）如图2，AD是△ABC的中线，G是AD上任意一点（点G不与A、D重合），过点G的直线交边AB于M′，交AC边的延长线于N′，若AG=aAD，AM′=bAB（a＞0，b＞0），请直接写出$\frac{N′C}{N′A}$的值（用含a、b的代数式表示）．

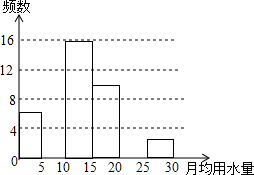11．八年级（2）班同学为了解2015年某小区家庭1月份用水情况，随机调查了该小区部分家庭，并将调查数据进行如下整理：

月均用水量x（t）	频数（户）	频率
0＜x≤5	6	0.12
5＜x≤10	a	0.24
10＜x≤15	16	0.32
15＜x≤20	10	0.20
20＜x≤25	4	b
25＜x≤30	2	0.04

（1）求出a，b的值，并把频数分布直方图补充完整．
（2）求月均用水量不超过15t的家庭数占被调查家庭总数的百分比．
（3）若该小区有1000户家庭，根据调查数据估计，该小区月均用水量超过20t的家庭大约有多少户？

10．如图，折叠直角三角形纸片的直角，使点C落在AB边上的点E处，已知BC=12，∠B=30°，则DE=4．