
科目: 来源: 题型:选择题
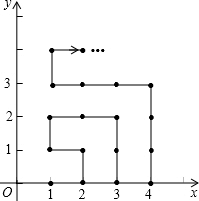 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )
如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“→”方向排序,如(1,0),(2,0)(2,1),(1,1)(1,2)(2,2),…,根据这个规律,第2015个点的横坐标为( )| A. | 44 | B. | 45 | C. | 46 | D. | 47 |
查看答案和解析>>
科目: 来源: 题型:选择题
 如图,相邻两线段互相垂直,两只蜗牛均同时从A点出发爬往C点,蜗牛甲沿着“A→B→C”路线走,蜗牛乙沿着“A→D→E→F→G→H→I→J→C”的路线走,若他们的爬行速度相同,则先到达点C的是( )
如图,相邻两线段互相垂直,两只蜗牛均同时从A点出发爬往C点,蜗牛甲沿着“A→B→C”路线走,蜗牛乙沿着“A→D→E→F→G→H→I→J→C”的路线走,若他们的爬行速度相同,则先到达点C的是( )| A. | 蜗牛甲 | B. | 蜗牛乙 | C. | 同时到达 | D. | 无法确定 |
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:选择题
| A. | x≥0 | B. | -3<x≤0 | C. | x>3 | D. | x>3或x<0 |
查看答案和解析>>
科目: 来源: 题型:解答题

查看答案和解析>>
科目: 来源: 题型:填空题
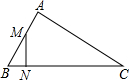 如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.
如图,△ABC中,M是AB的中点,N在BC上,BC=2AB,∠BMN=∠C,则△BMN∽△BCA,相似比为$\frac{1}{4}$,$\frac{BN}{NC}$=$\frac{1}{7}$.查看答案和解析>>
科目: 来源: 题型:解答题
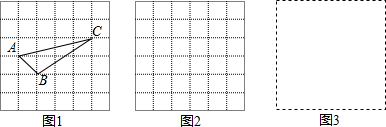
查看答案和解析>>
科目: 来源: 题型:解答题
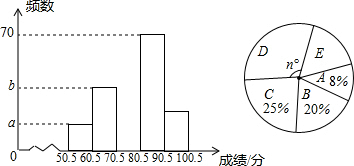
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com