科目： 来源： 题型：解答题

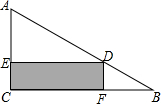20．如图，在Rt△ABC的内部作一个矩形CEDF，其中CE、CF在三角形的边AC、BC上，已知AC=6cm，BC=8cm．设长方形的面积为y m²，边长DE=x m．
（1）求y与x的函数关系式，写出x的取值范围；
（2）画出函数的图象；
（3）根据图象，判断当x为何值时，y的值最大？最大值是多少？

科目： 来源： 题型：解答题

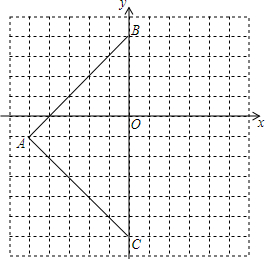19．如图，三角形ABC在平面直角坐标系中，三个顶点坐标分别为A（-5，-1）、B（0，4）、C（0，-6）．
（1）将三角形ABC向右平移3个单位，再向上平移1个单位得三角形A′B′C′，请在图中画出三角形A′B′C′，且点A′、B′、C′的坐标分别为A′（-2，0），B′（3，5），C′（3，-5）．
（2）三角形ABC与三角形A′B′C′不重合部分的面积和为42．

科目： 来源： 题型：解答题

18．如图，四边形ABCD中，∠A+∠B=200°，∠ADC、∠DCB的平分线相交于点O，求∠COD的度数．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

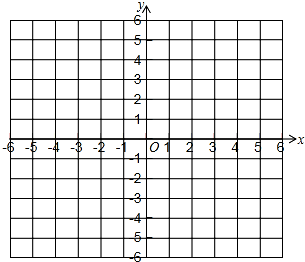16．已知：A（0，1），B（2，0），C（4，3）
（1）在坐标系中描出各点，画出△ABC．
（2）求△ABC的面积；
（3）设点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标．

科目： 来源： 题型：解答题

15．已知AB∥CD，图形中∠AEC与∠A、∠C有怎样的数量关系？并说明理由．请把以下推理过程补充完整：
解法一：∠AEC=∠A+∠C
理由：如图（一），过点E作直线EFAB．
∵AB∥CD，EF∥AB
∴CD∥EF
∵AB∥EF，EF∥CD
∴∠A=∠AEF，∠C=∠CEF
∴∠AEC=∠AEF+∠CEF=∠A+∠C．
解法二：∠AEC=∠A+∠C
理由：如图（二），延长AE交CD于点M．
∵AB∥CD
∴∠A=∠AMC．
又∵∠AEC是三角形EMC的外角．
∴∠AEC=∠AMC+∠C．
∴∠AEC=∠A+∠C．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

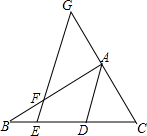13．请将下列证明过程补充完整：
已知：如图，AD是△ABC的角平分线，点E在BC上，点G在CA的延长线上，EG交AB于点F，且∠BEF+∠ADC=180°．
求证：∠AFG=∠G．
证明：∵∠BEF+∠ADC=180°（已知），
又∵∠BEF+∠GED=180°（平角的定义），
∴∠GED=∠ADC（等式的性质），
∴AD∥GE（同位角相等，两直线平行），
∴∠AFG=∠BAD（两直线平行，内错角相等），
且∠G=∠CAD（两直线平行，同位角相等），
∵AD是△ABC的角平分线（已知），
∴∠CAD=∠BAD（角平分线的定义），
∴∠AFG=∠G．

科目： 来源： 题型：解答题

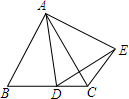12．已知△ABC是等边三角形，点D是BC边所在直线上的一个动点，以AD为边，作等边△ADE（点E始终在直线AD的右方），连接CE．
（1）当点D在BC边上，求证：BC=DC+CE；
（2）当点D在BC的延长线上时，BC=DC+CE是否成立，请说明理由；
（3）当点D在CB的延长线上时，上述结论是否成立？若不成立，请你画出符合条件的图形，并直接写出成立的结论．

科目： 来源： 题型：解答题

11．某中学甲、乙两位教师先后从学校出发，到距学校10km的培训中心参加新教材培训学习，图中I_甲，I_乙分别表示甲、乙两位教师从学校到培训中心所走的路程S（km）随时间t（分钟）变化的函数图象．
（1）求甲、乙两位教师的平均速度各是多少？
（2）求乙出发后追上甲所用的时间是多少？