
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.
如图,已知直线l的解析式是y=$\sqrt{3}$x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2…,按此作法继续下去,则点A2014的纵坐标为($\frac{4}{3}$)2014.查看答案和解析>>
科目: 来源: 题型:填空题
 如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.
如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.查看答案和解析>>
科目: 来源: 题型:选择题
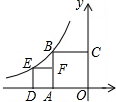 如图,点B,E是反比例函数y=-$\frac{4}{x}$(x<0)图象上的两点,点C在y轴上,点A,D在x轴上,且四边形OABC和四边形ADEF均为正方形,则点D的横坐标是( )
如图,点B,E是反比例函数y=-$\frac{4}{x}$(x<0)图象上的两点,点C在y轴上,点A,D在x轴上,且四边形OABC和四边形ADEF均为正方形,则点D的横坐标是( )| A. | -1-$\sqrt{5}$ | B. | -5+$\sqrt{5}$ | C. | -2$\sqrt{3}$ | D. | -1-2$\sqrt{2}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
 如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )
如图是正方形网格,除A,B两点外,在网格的格点上任取一点C,连接AC,BC,能使△ABC为等腰三角形的概率是( )| A. | $\frac{4}{23}$ | B. | $\frac{6}{23}$ | C. | $\frac{7}{23}$ | D. | $\frac{8}{23}$ |
查看答案和解析>>
科目: 来源: 题型:选择题
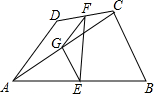 如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )
如图,在四边形ABCD中.AD=BC.E,F,G分别是AB,CD,AC的中点,若∠DAC=36°,∠ACB=84°,则∠FEG等于( )| A. | 20° | B. | 24° | C. | 26° | D. | 15° |
查看答案和解析>>
科目: 来源: 题型:解答题
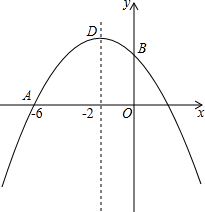 已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.
已知抛物线y=ax2-x+c过点A(-6,0),对称轴是直线x=-2,与y轴交于点B,顶点为D.查看答案和解析>>
科目: 来源: 题型:填空题
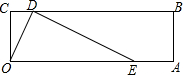 如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.
如图,四边形OABC是矩形,OA=3,OC=1,点D是线段BC上的动点(与端点B、C不重合),过点D作直线ED交线段OA于点E,tan∠DEO=$\frac{1}{2}$.若矩形OABC关于直线DE的对称图形为四边形O1A1B1C1,则四边形O1A1B1C1与矩形OABC的重叠部分的面积是$\frac{5}{4}$.查看答案和解析>>
科目: 来源: 题型:解答题
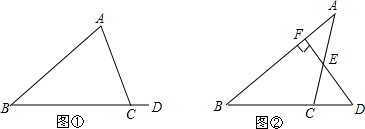
查看答案和解析>>
科目: 来源: 题型:填空题
 如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.
如图,不解关于x,y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$,请直接写出它的解$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com