科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

12．如图，⊙O的内接四边形ABMC中，AB＞AC，M是$\widehat{BC}$的中点，MH⊥AB于N，求证：BH=$\frac{1}{2}$（AB-AC）．

科目： 来源： 题型：选择题

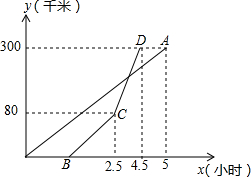11．甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发向乙地．如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系式；折线B-C-D表示轿车离甲地距离y（千米）与x（小时）之间的函数关系．下列四种说法：
①货车的速度为60千米/小时；
②轿车与货车相遇时，货车恰好从甲地出发了3.9小时；
③轿车比货车晚出发了1.8小时
④若轿车到达乙地后，马上沿原路以CD段速度返回，则轿车从乙地出发$\frac{3}{17}$小时再次与货车相遇．
其中正确的个数是（　　）

A．

1个

B．

2个

C．

3个

D．

4个

科目： 来源： 题型：解答题

10．如图1，在平面直角坐标系中，点A，B的坐标分别为A（m，0），B（n，0）且m、n满足|m+2|+$\sqrt{5-n}$=0，现同时将点A，B分别向上平移3个单位，再向右平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．
（1）求点C，D的坐标及四边形OBDC的面积；
（2）如图2，点P是线段BD上的一个动点，连接PC，PO，当点P在BD上移动时（不与B，D重合）$\frac{∠DCP+∠BOP}{∠CPO}$的值是否发生变化，并说明理由．．
（3）在四边形OBDC内是否存在一点P，连接PO，PB，PC，PD，使S_△PCD=S_△PBD；S_△POB：S_△POC=5：6，若存在这样一点，求出点P的坐标，若不存在，试说明理由． 

科目： 来源： 题型：解答题

科目： 来源： 题型：填空题

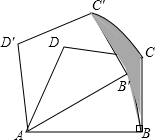8．如图，在四边形ABCD中，∠ABC=90°，∠BAC=30°，BC=6，将四边形ABCD绕点A逆时针旋转30°至四边形AB′C′D′处，则旋转过程中，边BC所扫过的区域（图中阴影部分）的面积为3π．

科目： 来源： 题型：解答题

7．如图，已知FG是∠EFC的角平分线，BG是∠ABC的角平分线，
（1）求证：∠BGF=$\frac{1}{2}$（∠AME+∠C）．
（2）若∠BAC=60°，∠FEC=80°，求∠BGF的度数．

科目： 来源： 题型：解答题

6．已知直线AB∥CD，分别探讨下面图①至图⑤，五个图形中∠A与∠E、∠C之间的数量关系，并说明理由．

科目： 来源： 题型：填空题