科目： 来源： 题型：填空题

10．在一次大型演出中，由1200名演员排出如图所示的正五边形队，内圈每边3人，往外每圈每边增加2人（即由内向外算起，第2圈每边5人，第三圈每边7人…），这样1200人恰好排完，则这个队共排了15圈．

科目： 来源： 题型：填空题

9．在图中，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第9个图案中共有81个小正方形

科目： 来源： 题型：选择题

科目： 来源： 题型：解答题

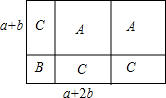7．如图，有足够多的正方形（A型和B型）和长方形（C型）卡片，利用这些卡片可以进行因式分解，如对多项式2a²+3ab+b²进行因式分解．
（1）要拼成面积为2a²+3ab+b²的图形需A卡2张，B卡1张，C卡3张，利用这些卡片可以拼成一个长方形（不重叠无缝隙），由于同一长方形面积的有不同表示形式：各卡片的面积和为2a²+3ab+b²，长与宽的积为（a+b）（a+2b），可以得到2a²+3ab+b²=（a+b）（a+2b）．
（2）请参考照（1）中的因式分解过程，画出草图对2a²+5ab+2b²进行因式分解．

科目： 来源： 题型：选择题

6．阅读材料：在△ABC中，有一点P，当P₁、A、B、C没有任何三点在同一直线上，可构成三个不重叠的小三角形（如图）．当△ABC内的点的个数增加时，若其它条件不变，三角形内互补重叠的小三角形的个数情况怎样？请观察图形和表格填空．表格中的空白处应填（　　）

△ABC内点的个数	1	2	3	…	12
构成不重叠的小三角形的个数	3	5	7	…

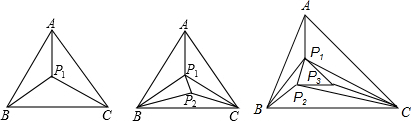
A．

21

B．

23

C．

25

D．

28

科目： 来源： 题型：解答题

5．如图，图（1）是一个扇形AOB，将其作如下划分：第一次划分：如图（2）所示，得到扇形的总数为6个，分别为：扇形AOB、扇形AOC、扇形COB、扇形A₁OB₁、扇形A₁OC₁、扇形C₁OB；第二次划分：如图（3）所示，在扇形C₁OB₁中，按上述划分方式继续划分，可以得到扇形的总数为11个；第三次划分：如图（4）所示；
依次划分下

（1）根据题意，完成表格

划分次数	扇形总个数
1	6
2	11
3	16
4	21
…	…
n	5n+1

（2）请判断，按上述方式继续划分，能否得到扇形的总数为2000个？为什么？

科目： 来源： 题型：填空题

4．如图，以直线x=-1为对称轴的二次函数y=ax²+bx+c经过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a-2b+c＞0；④若（-5，y₁）（$\frac{5}{2}$，y₂）是该二次函数图象上的两个点，则y₁＞y₂．其中说法正确的是①②④．（只填序号）

科目： 来源： 题型：解答题

3．如图用同样规格的正方形瓷砖铺设矩形地面，请观察下列图形并解答问题；
（1）在第n个图形中每一横行共有n+2块瓷砖，每一竖行共有n+1块瓷砖；（均用含n的代数式表示）
（2）按上述铺设方案，铺一块这样的矩形地面共用了420块瓷砖，求此时每一横行用了多少块瓷砖？

科目： 来源： 题型：解答题

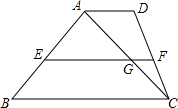2．在梯形ABCD中，AD∥BC，点E、F分别在边AB、CD上．EF∥BC，EF交AC于G．EB=DF，AE=9，CF=4．求BE，CD，$\frac{GF}{AD}$的值．

科目： 来源： 题型：解答题

1．如图，已知△ABC，AM是中线，点P在边AB上，点Q在边AC上，PQ交AM于点N．
（1）求证：$\frac{PB}{PA}$+$\frac{QC}{QA}$=$\frac{2MN}{NA}$；
（2）若$\frac{AP}{PB}$=m，$\frac{AQ}{QC}$=n，求$\frac{MN}{NA}$的值．