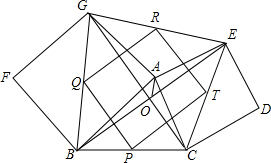9．如图，已知△ABC，分别以AB，AC为边作正方形ABFG和正方形ACDE，连接BE，CG交于点O，联结AO，P、Q、R、T分别是BC、BG、EG、CE的中点．
（1）求证：AO平分∠EOG；
（2）判断四边形PQRT的形状，并证明你的结论．

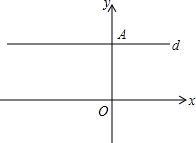8．如图，在平面直角坐标系中，点O为坐标原点，A（0，a），B（b，0），a与b为方程组$\left\{\begin{array}{l}{4a+3b=-11}\\{a+b=-5}\end{array}\right.$的解，过点A作x轴的平行线d
（1）求点A、B的坐标；
（2）动点P从B出发沿x轴正方形运动，速度为2个单位/秒，设运动时间为t秒，△POA的面积为S，求出用t表示S的关系式（并直接写出相应的t的取值范围）；
（3）在（2）的条件下，若动点Q同时从A出发沿射线AO方向运动，速度为4个单位/秒，在直线d上有动点R，问t为何值时，以P、Q、R为顶点的三角形是等腰直角三角形（PQ为底），并求出此时点P的坐标．

7．如图，在直角坐标系中，矩形OABC的两边在坐标轴上，其中点B的坐标为（4，3），过点A的直线AD的解析式为y=2x+3，点P是直线AD上一动点，点Q是线段BC（包括B，C两点）上一动点
（1）若AP⊥AQ，求AQ的解析式；
（2）以P，B，C为顶点作平行四边形PBEC，当对角线PE的值最小时，求点P的坐标；
（3）将直线y=2x+3向右平移3个单位，在该直线上存在点N，使△ANQ为等腰三角形，请直接写出平移后的直线解析式和所有满足条件的点N坐标．

6．如图，正方形ABCD中，AB=30，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G．连接AG、CF．下列结论：①△ABG≌△AFG；②BG=15；③△CFG是正三角形；④△FGC的面积为90．其中正确的是①②④（填所有正确答案的序号）．

5．将1、$\sqrt{2}$、$\sqrt{3}$、$\sqrt{6}$按下列方式排列，若规定（m、n）表示第m排从左向右第n个数．
（1）表示（5，4）与（15，7）表示的两数之积是多少？
（2）表示（100，10）的数是多少？

4．已知一次函数y=2x+b经过点A（0，-12），且与一次函数y=-x相交于点P．
（1）求b的值及点P的坐标；
（2）如图①，是否存在点D，是四边形OPBD为平行四边形？若存在，直接写出点D的坐标；若不存在，请说明理由．
（3）如图②，点M是线段OP上的一个动点（O、P两点除外），以每秒$\sqrt{2}$个单位长度的速度由点P向点O运动，过点M作直线MN∥x轴，交PB于点N，将△PMN沿直线MN对折，得到△P₁MN，在动点M的运动过程中，设△P₁MN与梯形OMNB的重叠部分的面积为S，运动时间为ts，求S关于t的函数关系式．

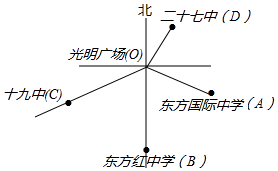3．小明在光明广场（点O）绘制了市内几座学校相对广场的位置简图，（图中1cm表示5km），东方红中学在广场正南方向，测得OA=1.7cm，OB=2cm，OC=2cm，OD=1.4cm，∠AOC=123°18′，∠BOA=68°24′，∠AOD=88°28′，如何确定每个学校的具体位置？

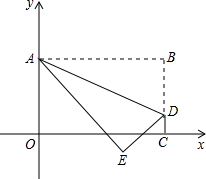2．将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C的坐标为（m，0）（m＞0），点D（m，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．
（1）当m=3时，点B的坐标为（3，4），点E的坐标为（0，1）；
（2）随着m的变化，试探索：点E能否恰好落在x轴上？若能，请求出m的值；若不能，请说明理由．
（3）如图，若点E的纵坐标为-1，且点（$2\sqrt{5}$，a）落在△ADE的内部，求a的取值范围．

1．已知：如图，在矩形ABCD中，BC=2$\sqrt{3}$，AB=6，在Rt△EOF中，∠FOE=90°，EO=4，EF=8，点E在CB的延长线上，点O与点B重合．现将Rt△EOF绕点O按顺时针方向旋转，OF与AD边交于点P，旋转时，点P以每秒$\sqrt{3}$个单位长度的速度沿AD运动，当点P到达点D时，Rt△EOF停止旋转运动，立即改为沿BC边以每秒$\sqrt{3}$个单位长度的速度向点C平移，当点O到达点C时，停止运动．设Rt△EOF的运动时间为x（秒）．
（1）当x为多少时，点P到达点D；
（2）Rt△EOF在运动过程中与矩形ABCD重合部分的面积为y，求y与x的函数关系式；
（3）在平移过程中，线段OE与AB的交点为M，是否存在某时刻x，使△MDO为等腰三角形？若存在，请直接写出；不存在，说明理由．

11．2a⁴-a³b²-5ab³+a²-1是五次五项式，它的最高次项是-a³b²，常数项是-1．