15．小明用力地将篮球向篮筐抛出.篮球离地的高度h的关系可以表示为:h=v0t-$\frac{1}{2}$gt2+h0(其中v0表示篮球离开时的速度.g表示重力加速度.g=10(m/s2).h0表示篮——青夏教育精英家教网—

相关习题

0 310047 310055 310061 310065 310071 310073 310077 310083 310085 310091 310097 310101 310103 310107 310113 310115 310121 310125 310127 310131 310133 310137 310139 310141 310142 310143 310145 310146 310147 310149 310151 310155 310157 310161 310163 310167 310173 310175 310181 310185 310187 310191 310197 310203 310205 310211 310215 310217 310223 310227 310233 310241 366461

科目： 来源： 题型：解答题

15．小明用力地将篮球向篮筐抛出，篮球离地的高度h（m）与时间t（s）的关系可以表示为：h=v₀t-$\frac{1}{2}$gt²+h₀（其中v₀表示篮球离开时的速度，g表示重力加速度，g=10（m/s²），h₀表示篮球离手时的速度），如果v₀=9（m/s），h₀=2（m），求：
（1）篮球抛出到落地需要多少时间？
（2）篮球离地最高有多少米？

查看答案和解析>>

科目： 来源： 题型：解答题

14．

如图：∠ADC+∠AEB=180°，AB=k•AC，判断BE与CD的关系，并加以证明．

查看答案和解析>>

科目： 来源： 题型：解答题

13．在梯形ABCD中，AD∥BC，AB⊥BC，AD=2，AB=3，BC=6．
（1）求sinC的值；
（2）如图，P为边CD上的一个动点，直线EF过点P，交射线AD于E，交边BC于F，且∠DPB=∠EFB．设DP=x，CF=y．
①求y关于x的函数解析式，并写出定义域；
②在边CD上是否存在点P，使得△DEP∽△BPF？如果存在，求出x的长；如果不存在，说明理由．

查看答案和解析>>

科目： 来源： 题型：填空题

12．矩形的一边长是6，对角线是10，则这个矩形的面积是48．

查看答案和解析>>

科目： 来源： 题型：解答题

11．

如图，在矩形ABCD中，AB=3，BC=6，且BE=2EC，DM⊥AE于M．求sin∠MAD的值．

查看答案和解析>>

科目： 来源： 题型：解答题

10．

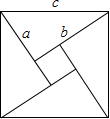勾股定理是一条古老的数学定理，它神秘而美妙．著名数学家华罗庚曾提出把“数形关系”（勾股定理）带到其他星球，作为地球人与其他星球“人”进行第一次“谈话”的语言．它有很多种证明方法，其技巧各有不同．我国汉代数学家赵爽就根据弦图，利用面积法进行了证明．请你根据右图证明勾股定理．

查看答案和解析>>

科目： 来源： 题型：解答题

9．

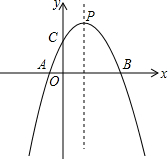如图，抛物线y=-x²+bx+c的对称轴是直线x=1，与y轴交于点C（0，3），与x轴交于 A，B两点．
（1）请写出这个抛物线的解析式；
（2）若此抛物线与x轴交于A，B两点，顶点是P，求△ABP的面积．
参考公式：顶点坐标（-$\frac{b}{2a}$，$\frac{4ac-{b}^{2}}{4a}$）

查看答案和解析>>

科目： 来源： 题型：填空题

8．抛物线y=ax²+bx+c（a≠0）的图象与x轴只交于一点（-3，0），则关于x的方程ax²+bx+c=0的根是x=-3．

查看答案和解析>>

科目： 来源： 题型：填空题

7．抛物线y=x²+mx-2m²（m≠0）与x轴的交点的个数是2．

查看答案和解析>>

科目： 来源： 题型：解答题

6．已知抛物线y=x²-ax+2（a-3）．
（1）求证：不论a为何实数，这个抛物线与x轴总有两个交点；
（2）如果有一交点坐标为（3，0），求a的值．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学