14．菱形ABCD中，AB=6，∠BAC=45°，M为AB上一定点（AM），N，P分别为BC、AC上的动点，则MP+NP的最小值为6．

13．抛物线y₁=-2（x-4）²．
（1）写出y₁关于x轴对称的y₂和关于y轴对称的y₃的解析式；
（2）设y₁与y轴交于点A，y₂与y轴交于点B，y₁与y₃的顶点分别为点C、D，探索四边形ABCD的形状．

12．（1）如图①，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠C＞∠B，试探索∠DAE与∠B、∠C的关系；
（2）当图①变为图②时，（1）中的结论是否成立？为什么？
（3）当图②变为图③时，∠DFE与∠B、∠C的关系怎样？（直接写出结论）
（4）当图③变为图④时，∠DFE与∠B、∠C的关系怎样？（直接写出结论）

11．如图，在平面直角坐标系中，O为坐标原点，B的坐标（5，0），M为等腰梯形OBCD底边OB上一点，OD=BC=2，∠DMC=∠DOB=60°
（1）求直线CB的解析式；
（2）求点M的坐标；
（3）∠DMC绕点M顺时针旋转a（30°＜a＜60°）后，得到∠D₁MC₁（点D₁、C₁依次与点D、C对应），射线MC₁交直线CB于点F．设DE=m，BF=n，求m与n的函数关系式．

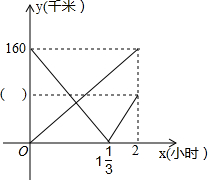10．甲乙两地相距240千米，一辆货车从甲地出发驶往乙地，货车行驶一段时间后，一辆轿车从乙地出发驶往甲地，两车与途中一服务区的距离y（千米）与轿车出发时间x（小时）之间的函数关系如图所示：
（1）求货车和轿车的速度；
（2）补全图中（　　）中的内容，求轿车与途中服务区的距离y（千米）与轿车出发时间x（小时）之间的函数关系；
（3）求货车出发多长时间后两车相遇．

9．有A，B两种机器人都被用来搬运化工物品，1台A型机器人和1台B型机器人共搬运150件物品，2台A型机器人和3台B型机器人共搬运360件物品．
（1）A，B两种机器人每台分别搬运多少件物品；
（2）搬运公司共派出A，B两种机器人共100台参与某搬运任务，A型机器人负责将物品从甲地搬到乙地，B型机器人再负责将其中部分物品从乙地搬到丙地，已知一件物品从甲地搬到乙地搬运公司可收入50元，从乙地搬到丙地搬运公司可收入150元，搬运费以乙，丙两地最终得到的件数收费，应安排A型机器人为多少台时，搬运公司可获得最大收入．

8．小华早晨从家出发匀速步行上学，小华在已步行200米时，爷爷发现小华的眼镜忘在家里，随即出发步行送眼镜去学校．小华到学校后发现眼镜未带上，立即原路返回，途中与爷爷相遇，如图是小华与爷爷之间的距离y米与爷爷出发时间x分钟之间的函数关系图，则小华家到学校的距离为多少米？

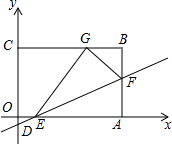7．如图，矩形OABC的边OA在x轴上，边OC在y轴上，点B在第一象限，直线y=$\frac{1}{3}$x-1与x轴、y轴、边AB分别交于点E，点D，点F，将△AEF沿直线EF折叠，点A恰好落在BC边的点G位置上，线段AF，BF的长是一元二次方程x²-9x+20=0的两根（AF＞BF）．
（1）求点E，点F的坐标；
（2）求直线EG的解析式；
（3）如果点N在直线EG上，那么在直线EF上存在一点M，使以点O，点E，点M，点N为顶点的四边形为平行四边形？若存在，请直接写出点M，点N的坐标；若不存在，请说明理由．

6．如图1所示，直线y=2x+b与x轴交于点E，与y轴交于点A，△AOE的面积为4，点D是直线AE在第一象限上的一点，以AD为边，在第一象限内作等腰Rt△ADC．
（1）求b的值；
（2）若AD=AE，试求点C的坐标；
（3）如图2，设直线AC交x轴于点P，当D点在第一象限内沿直线AE运动时，其他条件不变，P点位置是否发生改变？如果不变，请求出P点坐标；如果改变，请指出P点移动的范围．

5．某市高新技术产业开发区2013年初引进一个大型项目，计划总投资24亿元，建设起止年限为2013-2016，到2014年底累计完成投资达到5亿元．已知：项目建设方2013年只用自有资金投入，全年完成投资比2014年少$\frac{3}{4}$．
（1）求2013年项目建设方自有资金投入额；
（2）从2014年开始，项目建设方每年可以向银行抵押贷款或向其他金融机构发行定向债券募集资金，2014年由于资金紧张项目建设方除自有资金投入与银行贷款外，还向其他金融机构发行定向债券2.4亿元，2015年项目建设方自由资金投入仅占当年银行贷款的12%，并且向其他金融机构发行了定向债券6.64亿元，已知2013-2015年项目建设方每年自有资金投入减少的百分数是m，2014-2016年，银行贷款平均每年增加的百分数是5m，请通过计算说明，2016年项目建设方资金紧张状况是否有所缓解？