
科目: 来源: 题型:选择题
 如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )| A. | ①③ | B. | ①②④ | C. | ①②③④ | D. | ①③④ |
查看答案和解析>>
科目: 来源: 题型:解答题
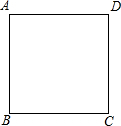 如图,正方形ABCD的面积和周长分别为S(cm)和C(cm),若长方形ABCD满足$\frac{S}{C}$=m,$\frac{AD}{AB}$=n,则称“m,n为长方形ABCD的特征数”.如,当AB=4,AD=12,$\frac{S}{C}$=$\frac{4×12}{2(4+12)}$=$\frac{3}{2}$,$\frac{AD}{AB}$=3,则长方形ABCD的特征数为“$\frac{3}{2}$,3”.
如图,正方形ABCD的面积和周长分别为S(cm)和C(cm),若长方形ABCD满足$\frac{S}{C}$=m,$\frac{AD}{AB}$=n,则称“m,n为长方形ABCD的特征数”.如,当AB=4,AD=12,$\frac{S}{C}$=$\frac{4×12}{2(4+12)}$=$\frac{3}{2}$,$\frac{AD}{AB}$=3,则长方形ABCD的特征数为“$\frac{3}{2}$,3”.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
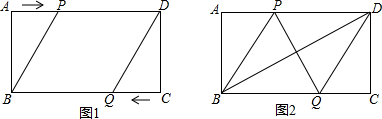
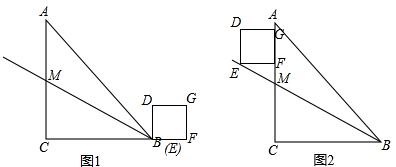
 已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.
已知:如图,在直角梯形ABCD中,AD∥BC,AB⊥BC,BC=9,∠C=60°,将一个30°角的顶点P放在DC边上滑动(P不与D,C重合),保持30°角的一边平行于BC,与边AB交于点E,30°角的另一边与射线CB交于点F,联结EF.查看答案和解析>>
科目: 来源: 题型:填空题
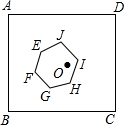 如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$.
如图,正方形ABCD的边长为1,中心为点O,有一边长大小不定的正六边形EFGHIJ绕点O可任意旋转,在旋转过程中,这个正六边形始终在正方形ABCD内(包括正方形的边),当这个正六边形的边长最大时,AE的最小值为$\frac{\sqrt{2}-1}{2}$.查看答案和解析>>
科目: 来源: 题型:填空题
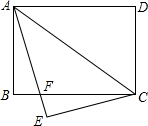 如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.
如图,矩形ABCD中,AB=6,BC=8,将△ACD沿对角线AC翻折得△ACE,AE交BC于点F,将△CEF绕点C逆时针旋转α角(0°<α<180°)得△CE′F′,点E、F的对应点分别为E、F的对应点分别为E′、F′.旋转过程中直线CF′、E′F′分别交直线AE于点M、N,当△F′NM是等腰三角形且MN=MF′时,则MN=$\frac{275}{56}$.查看答案和解析>>
科目: 来源: 题型:解答题
 A、B、C三地依次为同一高速公路上的三个城市,某天,甲、乙两车分别从A地、C地同时出发,匀速前进,并相约同时到达B地,甲车匀速行驶一段时间后,中途因故停留一段时间后,再以另一速度匀速前进,结果甲乙两车仍恰好在相约时间到达B地,如图y1、y2分别是甲、乙两车行驶的路程y(km)与所用时间x(h)的函数图象.求A、B两地距离.
A、B、C三地依次为同一高速公路上的三个城市,某天,甲、乙两车分别从A地、C地同时出发,匀速前进,并相约同时到达B地,甲车匀速行驶一段时间后,中途因故停留一段时间后,再以另一速度匀速前进,结果甲乙两车仍恰好在相约时间到达B地,如图y1、y2分别是甲、乙两车行驶的路程y(km)与所用时间x(h)的函数图象.求A、B两地距离.查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
查看答案和解析>>
科目: 来源: 题型:解答题
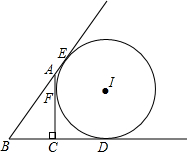 如图,△ABC,∠ACB=90°,⊙I与△ABC的AC边、BA和BC的延长线分别相切于点F、E、D,
如图,△ABC,∠ACB=90°,⊙I与△ABC的AC边、BA和BC的延长线分别相切于点F、E、D,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com