科目： 来源： 题型：解答题

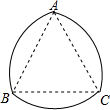10．如图所示的图形叫弧三角形，又叫莱洛三角形，是机械学家莱洛首先进行研究的，弧三角形是这样画的：先画正三角形ABC，然后分别以点A，B，C为圆心，AB长为半径画弧，若正三角形ABC的边长为2cm，求弧三角形的周长．

科目： 来源： 题型：解答题

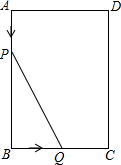9．如图在矩形ABCD中，AB=8cm，Bc=6cm，动点P，Q分别从A，B向B、C运动，运动速度为1cm/s，当P、Q一点停止运动则另一点停止运动．设△PBQ的面积为y，点P、Q运动时间为x（s）．
（1）求y与x的函数关系；
（2）当x为多少时，五边形APQCD的面积最小，并求最小面积．

科目： 来源： 题型：选择题

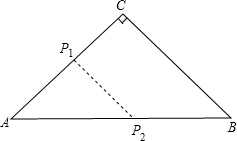8．如图所示，△ABC为等腰直角三角形，P₁，P₂分别从A，B出发，速度都是1cm/s，P1运动到C为止，AB=100cm，t（s）后，S${\;}_{△A{P}_{1}{P}_{2}}$的面积与t（s）的函数关系为（　　）

A．

S=t（100-t）

B．

S=$\frac{\sqrt{2}}{2}{t}^{2}-5\sqrt{2}t$

C．

S=$\frac{\sqrt{2}}{2}{t}^{2}$

D．

S=-$\frac{\sqrt{2}}{4}{t}^{2}+25\sqrt{2}t$

科目： 来源： 题型：解答题

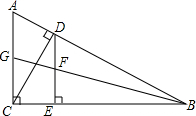7．如图，Rt△ABC中，∠ACB=90°，CD⊥AB于D，过点D作DE⊥BC，△BDE边DE上的中线BF延长线交AC于点G．
（1）证明：△ACD∽△DBE；
（2）证明：G为AC中点；
（3）求证：AD•BD=CE•CB；
（4）若AG=FG，求BF：GF；
（5）在（4）的条件下，若BC=6$\sqrt{2}$，求BD的长度．

科目： 来源： 题型：解答题

6．如图，已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm，AC与MN在同一直线上，开始时点A与点M重合，让△ABC沿着MN方向以每秒1cm的速度移动，最后点A与点N重合．
（1）直接写出重叠部分周长y（cm）与运动时间x（秒）之间的函数关系式及自变量x的取值范围；
（2）当运动时间为多少秒时，重叠部分周长等于△ABC周长的一半．（结果精确到1秒）

科目： 来源： 题型：解答题

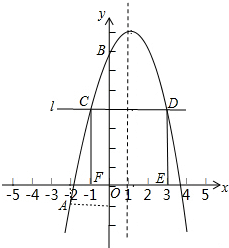5．如图，已知二次函数y=-x²+bx+c的图象经过A（-2，-1），B（0，7）两点．
（1）求该抛物线的解析式及对称轴；
（2）在x轴上方作平行于x轴的直线l，与抛物线交于C，D两点（点C在对称轴的左侧），过点C，D作x轴的垂线，垂足分别为F，E．当矩形CDEF为正方形时，求C点的坐标；
（3）在（2）的前提下，能否在y轴上找一点P，使|PC-PE|最小？若能，求出点P的坐标；若不能，说明理由．

科目： 来源： 题型：解答题

科目： 来源： 题型：选择题

3．有如图所示的几种几何体：

将它们按截面形状分成两类时，下面的分法不正确的是（　　）

	A．	截面可能是圆和三角形两类		B．	截面可能是圆和四边形两类
	C．	截面可能是圆和五边形两类		D．	截面可能是三角形和四边形两类

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题