8．△ABC绕点B逆时针旋转90°得到△DBE，若恰好得到C，E，D三点共线，则AC、BC、CD的数量关系是$\sqrt{2}$BC+AC=CD．

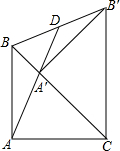7．已知，在等腰三角形ABC中，AB=AC，∠BAC=90°，将△ABC绕点C旋转45°成为Rt△CA′B′，连接AA′并延长交BB′于点D，求证：BD=B′D．

6．如图，正方形ABCD中，E，F分别是BC，CD边上的点，AE，DE，BF，AF把正方形分成8小块，试比较S₃与S₂+S₇+S₈的大小，并说明理由．

5．抛物线y=ax²+bx+c的顶点为D（-1，-3），与x轴的一个交点A在点（-3，0）和（-2，0）之间，其部分图象如图所示，则以下结论：①abc＞0；②a+b+c＜0；③a-c=3；④方程以ax²+bx+c+3=0有两个的实根，其中正确的个数为（　　）

A．

1

B．

2

C．

3

D．

4

4．如图，正方形ABCD中，AB=3，点E在边CD上，且CD=3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG，CF．下列结论：
①点G是BC中点；②FG=FC；③EF=FC；④∠GAE=45°；⑤S_△FGC=$\frac{9}{10}$．
其中正确的有（　　）

A．

2个

B．

3个

C．

4个

D．

5个

3．如图，有一边长为5cm的正方形ABCD和等腰Rt△PQR，QR=8cm，点B、C、Q、R在同一条直线上，当C、Q两点重合时，△PQR以1cm/秒的速度向左开始匀速运动，设与正方形重合部分的面积为S cm²．
（1）求S与运动时间t（秒）的函数关系式，并指出自变量的取值范围；
（2）求S的最大值．

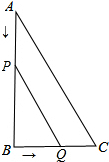2．如图，在三角形ABC中，∠B=90°，AB=22cm，BC=20cm，点P从点A出发沿AB边向点B以2cm/s的速度移动，点Q从点B出发沿BC边向点C以1cm/s的速度移动，P、Q分别从A，B同时出发．
（1）当P，Q的运动时间2（s）时，线段BP=18cm，线段BQ=2cm，三角形PBQ的面积S=18cm²．
（2）当P，Q的运动时间x（s）（x≤11）时，线段BP=（22-2x）cm，线段BQ=xcm，三角形PBQ的面积S=（-x²+11x）cm²；
（3）当P，Q的运动时间n（s）（n≤11）时，四边形APQC的面积y=n²-11n+110．

1．已知任意四边形ABCD，边AD、BC的中点分别为E、F，求证：$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AB}$$+\overrightarrow{DC}$）．

20．已知二次函数图象与x轴交于A、B两点（A在B的左侧），与y轴交于点C，顶点是点D，其中A（-1，0），C（0，-3），对称轴是直线x=1．
（1）求二次函数的解析式；
（2）若E为抛物线上一个动点，直接写出△ABE的面积S与E点的个数存在怎样的关系？
（3）若P（x，y）为抛物线上一个动点（0＜x＜3），当点P运动到什么位置时，四边形ABPC的面积最大，求出此时P点的坐标和ABPC的最大面积；
（4）若Q为抛物线上一个动点，是否存在Q，使得△BCQ为以BC为直角边的直角三角形？如果存在，求出Q点坐标；如果不存在，请说明理由．

19．某小贩每天从批发市场买进一定数量的土豆，其价格为每千克0.60元，卖出的价格是每千克0.80元，卖不掉的土豆可卖给附近的餐厅，不过每千克卖出的价格P（元/千克）与卖出的数量x（千克）的关系可近似地用图中的一条折线表示．经过市场调查发现，在一个月内（按30天算）有20天每天可卖出100千克，有10天每天只能卖出70千克，而批发市场规定每天批发给小贩的它的数量必须相同．
（1）求出价格P（元/千克）与卖给餐厅的土豆数量x（千克）之间的关系式．
（2）设每天小贩从批发市场批发土豆的数量为x（千克），每月所得的毛利润为W（元）．
①根据具体的x（千克）的值，填写下表：

所批发土豆的数量x（千克）	70	90	100
每月所得毛利润W（元）	420	540	570

②该小贩每天从批发市场买进多少千克土豆才能使每月所获得利润最大？最多可赚多少钱？