2．如图，在△ABC中，CD是AB边的中线，∠CDB=60°，将△BCD沿CD折叠，使点B落在点E的位置．证明：△ADE是等边三角形．

1．已知：$\frac{a}{b}=\frac{c}{d}=\frac{e}{f}=4$，且a+c+e=8，则b+d+f等于（　　）

A．

4

B．

8

C．

32

D．

2

20．【问题情境】
如图1，P是⊙O外的一点，直线PO分别交⊙O于点A、B
小明认为线段PA是点P到⊙O上各点的距离中最短的线段，他是这样考虑的：在⊙O上任意取一个不同于点A的点C，连接OC、CP，则有OP＜OC+PC，即OP-OC＜PC，由OA=OC得OP-OA＜PC，即PA＜PC，从而得出线段PA是点P到⊙O上各点的距离中最短的线段
小红认为在图1中，线段PB是点P到⊙O上各点的距离中最长的线段，你认为小红的说法正确吗？请说明理由

【直接运用】
如图3，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是$\widehat{CD}$上的一个动点，连接AP，则AP的最小值是$\sqrt{5}$-1
【构造运用】
如图4，在边长为4的菱形ABCD中，∠A=60°，M是AD边的中点，N是AB边上一动点，将△AMN沿MN所在的直线翻折得到△A′MN，连接A′C，请求出A′C长度的最小值
解：由折叠知A′M=AM，又M是AD的中点，可得MA=MA′=MD，做点A′在以AD为直径的圆上，如图5，以点M为圆心，MA为半径画⊙M，过M作MH⊥CD，垂足为H（请继续完成本题的后续解题过程）

【深度运用】
如图6，△ABC、△EFG均是边长为4的等边三角形，点D是边BC、EF的中点，直线AG、FC相交于点M，当△EFG绕点D旋转时，则线段BM长的最小值和最大值分别是2$\sqrt{3}$-2和2$\sqrt{3}$+2．

19．如图1，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，$\widehat{AE}$=$\widehat{AB}$，BE分别交AD、AC于点F、G
（1）判断△FAG的形状，并说明理由；
（2）如图2，若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由；
（3）在（2）的条件下，若BG=10，BD-DF=1，求AB的长．

18．某企业信息部进行市场调查发现：
信息一、如果单独投资A种产品，所投资利润yA（万元）与投资金额x（万元）之间存在某种关系的部分对应值如下表：

x（万元）	1	2	2.5	3	5
yA（万元）	0.4	0.8	1	1.2	2

信息二：如果单独投资B种产品，则所获利润y_B（万元）与投资金额x（万元）之间存在二次函数关系：y_B=ax²+bx，且投资2万元时获利润2.4万元，当投资4万元时，可获利润3.2万元．
（1）从所学过的函数中猜想y_A与x之间的关系，并求出y_A与x的函数关系式；
（2）求出y_B与x的函数关系式，并求想利润y_B为3（万元）应投资金额；
（3）如果企业同时对A、B两种产品共投资15万元，请设计一个能获得最大利润的投资方案，并求出按此方案能获得的最大利润是多少？

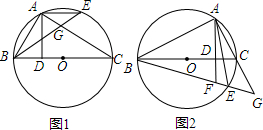
17．已知二次函数y=ax²+bx+c的图象如图所示，则下列结论：①ac＞0；②a+b=0；③当x＜$\frac{1}{4}$时，y随x增大而增大；④a-b+c＜0，其中正确的个数有（　　）

A．

4个

B．

3个

C．

2个

D．

1个

16．将长方形纸片ABCD按如下顺序进行折叠：对折、展平，得折痕EF（如图①）；沿GC折叠，使点B落在EF上的点B′处（如图②）；展平，得折痕GC（如图③）；请你求出图②中∠BCB′的度数．

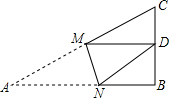15．如图，Rt△ABC中，∠B=90°，AB=9，BC=6，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段AN的长等于（　　）

A．

3

B．

4

C．

5

D．

6

14．在△ABC中，AB=AC，∠B=60°，BC=2cm，则AC的长为2cm．

13．在△ABC中，其中两边边长为2、3，则周长m的取值范围是6＜m＜10．