2．如图，在等边三角形△ABC中，AE=CD，AD、BE交于P点，BQ⊥AD于Q，
（1）求证：BP=2PQ；
（2）连PC，若BP⊥PC，求$\frac{AP}{PQ}$的值．

1．如图，在Rt△ABC中，∠B=90°，将AB边沿AD折叠，使点B与点E重合，若AB=8，BC=6，则CD=$\frac{10}{3}$．

20．如图，网格中的每一个方格的边长都相等，点A，B，C都在网格的格点上，按要求完成下列各小题．
（1）画线段AB，延长线段BA到点D，使得DA=AB；
（2）在（1）的基础上，连接CB，CD，组成三角形BCD，并在图中画出三角形BCD绕点C顺时针旋转90°后得到的三角形B′CD′．

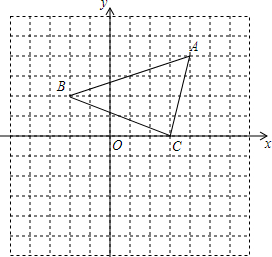19．如图，A（4、4），B（-2，2），C（3，0），
（1）画出它的以原点O为对称中心的△A′B′C′；
（2）写出A′，B′，C′三点的坐标；
（3）把每个小正方形的边长看作1，试求△ABC的面积．

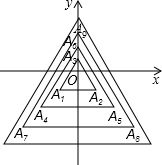18．如图，所有正三角形的一边平行于x轴，一顶点在y轴上，从内到外，它们
的边长依次为2，4，6，8，…，顶点依次用A₁、A₂、A₃、A₄、…表示，其
中A₁A₂与x轴、底边A₁A₂与A₄A₅、A₄A₅与A₇A₈、…均相距一个单位，则顶点A₂₅的坐标是（-9，-9）．

17．在9月份刚刚结束的女排世界杯中，中国女排在损兵折将的不利局面下，时隔十二年再夺世界杯冠军．为给中国队加油，中国某公司组织部分员工到日本名古屋现场观看了最后一场同日本队的比赛，已知该公司购买了每张3000日元和每张4000日元的门票共8张，总费用为27000日元．请问该公司购买了这两种门票各多少张？

16．已知在平面直角坐标系中有三点A（-2，1）、B（3，1）、
C（2，3）．请回答如下问题：
（1）在坐标系内描出点A、B、C的位置，并求△ABC的面积；
（2）在平面直角坐标系中画出△A′B′C′，使它与△ABC关于x轴对称，并写出△A′B′C′三顶点的坐标．

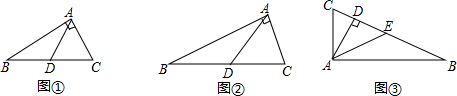
15．如图，点P是AB上任一点，∠ABC=∠ABD，从下列各条件中补充一个条件，不一定能推出△APC≌△APD的是（　　）

A．

BC=BD

B．

∠ACB=∠ADB

C．

AC=AD

D．

∠CAB=∠DAB

14．课本等腰三角形的轴对称性一节，我们最后通过直角三角形纸片折叠发现了定理“直角三角形斜边上的中线等于斜边的一半”．
（1）小聪同学画出了如图①所示的一个特殊的直角三角形，其中∠BAC为直角，AD为斜边BC上的中线，∠B=30°．它证明上面定理思路如下：延长AD至点E，使DE=AD，连结BE，再证△ABC≌△BAE，你认为小聪能否完成证明？能（只需要填“能”或“不能”）；
（2）小聪同学还想借助图②，任意的Rt△ABC为直角，AD为斜边BC上的中线，证明或推翻结论AD=$\frac{1}{2}$BC，请你帮助小聪同学完成；
（3）如图③，在△ABC中AD⊥BC，垂足为D，如果CD=1，AD=2，BD=4，求△ABC的中线AE的长度．

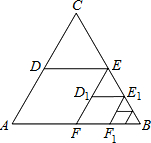13．如图，△ABC是边长为1的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作S₁；取BE中点E₁，作E₁D₁∥FB，E₁F₁∥EF，得到四边形E₁D₁FF₁，它的面积记作S₂．照此规律作下去，则S₂₀₁₅=$\frac{\sqrt{3}}{8}$×$\frac{1}{{4}^{2014}}$．