10．已知y=（a-2）x^|a|是y关于x的二次函数，则a=-2．

9．在同一平面坐标系中，抛物线y=-x²+2x-3通过平移得到的抛物线为y=-x²-4x+1，下面对抛物线y=-x²+2x-3平移得到的抛物线y=-x²-4x+1的描述正确的是（　　）

	A．	向右平移3个单位，再向上平移7个单位
	B．	向左平移3个单位，再向上平移7个单位
	C．	向右平移3个单位，再向下平移7个单位
	D．	向左平移3个单位，再向下平移7个单位

8．下面是小雷在一次测验中解答的填空题：
①若x²=m²，则x=m；
②方程3x（2x-1）=2x-1的解是$x=\frac{1}{3}$；
③已知三角形的两边分别为3和10，第三边长是方程x²-16x+63=0的根，则这个三角形的周长为20或22．
其中答案完全正确的题目个数是（　　）

A．

3

B．

2

C．

1

D．

0

7．有下列二次函数：
①y=-x²+2；②y=2x²-4x+2；③y=x²；④y=-x²+2x+3；⑤$y=\frac{1}{2}{x^2}-7$；⑥$y=-\frac{1}{2}{x^2}+x-\frac{1}{2}$．
其图象的顶点在y轴上的个数为（　　）

A．

2个

B．

3个

C．

4个

D．

5个

6．已知-1是关于x的一元二次方程x²+x-a=0的一个根，则a的值是（　　）

A．

3

B．

2

C．

-1

D．

0

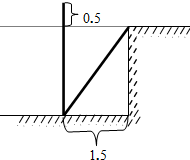5．如图，小刚准备测量一条河的深度，他把一根竹竿垂直插到离岸边1.5米远的水底（不计淤泥深度），竹竿高出水面0.5米，再把竹竿的顶端拉向岸边，竿顶和岸边的水面刚好相齐；请推断河水的深度为几米？

4．画出如图所示的几何体的三视图．

3．解方程：
（1）x（2x-5）=4x-10
（2）2x²-x-1=0
（3）x²+10x+9=0．

2．下列方程中，是关于x的一元二次方程为（　　）

	A．	3x+1=5x+7		B．	$\frac{1}{{x}^{2}}$+x-1=0
	C．	x2-5=0		D．	ax2-bx=5（a和b为常数）

1．操作：小明准备制作一个制作棱长为1cm的正方体纸盒，现选用一些废弃的纸片进行如下设计：

说明：方案一：图形中的圆过点A、B、C；    
     方案二：直角三角形的两直角边与展开图左下角的正方形边重合，斜边经过两个正方形的顶点．
     方案三中的每条边均过其中两个正方形的顶点．
纸片利用率=$\frac{纸片被利用的面积}{纸片的总面积}$×100%
发现：（1）小明发现方案一中的点A．B恰好为该圆一直径的两个端点．你认为小明的这个发现是否正确，请说明理由．
（2）小明通过计算，发现方案一中纸片的利用率约为38.2%，你知道怎么算的吗？请你写出他的计算过程；
（3）对于方案二纸片的利用率，小明认为关键的是要求出此直角三角形的两直角边的长，你是这样想的吗？请你选用合适的方法求出方案二纸片的利用率．（结果精确到0.1%）
探究：
（4）小明感觉上面两个方案的利用率均偏低，又进行了新的设计（方案三），请直接写出方案三的利用率：49.9%．（结果精确到0.1%）