科目： 来源： 题型：选择题

11．如图，在△ABC中，若AD⊥BC，点E是BC边上一点，且不与点B、C、D重合，则AD是几个三角形的高线（　　）

A．

4个

B．

5个

C．

6个

D．

8个

科目： 来源： 题型：选择题

10．如图，△ABE≌△ACF．若AB=5，AE=2，BE=4，则CF的长度是（　　）

A．

2

B．

5

C．

4

D．

3

科目： 来源： 题型：选择题

9．如图，将△AOB绕点O按逆时针方向旋转60°后得到△A′OB′，若∠AOB=25°，则∠AOB′的度数是（　　）

A．

60°

B．

45°

C．

35°

D．

25°

科目： 来源： 题型：解答题

8．如图，抛物线y=ax²+bx+2经过点A、B，且12a+10=0，正方形OABC的AB边上的动点P以2cm/s的速度由A向点B运动，同时，点Q由点B开始沿BC边以1cm/s的速度向点C移动，设运动时间为ts．
（1）求抛物线的解析式；
（2）t为何值时，PQ∥AC？
（3）设S=PQ²，试写出S与t的函数关系式，并写出t的取值范围；
（4）在（3）中，当S取最小值时，在抛物线上有点R，使得以P、B、Q、R为顶点的四边形是平行四边形，直接写出点R坐标（$\frac{12}{5}$，$\frac{6}{5}$）．

科目： 来源： 题型：填空题

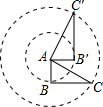7．如图，Rt△ABC中，AC=$\sqrt{5}$，以点A为中心逆时针旋转90°得到Rt△AB′C′，则Rt△A′B′C′，则$\widehat{CC′}$的长为$\frac{\sqrt{5}}{2}$π．

科目： 来源： 题型：解答题

6．如图，A、B、C三点表示三个村庄，线段AB、BC、AC表示村村通公路，为解决村民手机信号问题，移动通信公司计划新建一座基站和一间物资储备室．要求基站到这三个村庄的距离相等，物资储备室到这三条村村通公路的距离相等，请你在图中用尺规作图的方式确定基站和物资储备室的位置（分别用点P和Q表示，作图不写作法，但要保留作图痕迹）．

科目： 来源： 题型：解答题

科目： 来源： 题型：解答题

4．已知直线y=kx+3（k＜0）分别交x轴、y轴于A、B两点，线段OA上有一动点P由原点O向点A运动，速度为每秒1个单位长度，过点P作x轴的垂线交直线AB于点C，设运动时间为t秒．
（1）当k=-1时，线段OA上另有一动点Q由点A向点O运动，它与点P以相同速度同时出发，当点P到达点A时两点同时停止运动（如图1）．
①直接写出t=1秒时C、Q两点的坐标；
②若以Q、C、A为顶点的三角形与△AOB相似，求t的值．
（2）当k=-$\frac{3}{4}$时，设以C为顶点的抛物线y=（x+m）²+n与直线AB的另一交点为D（如图2），
①求CD的长；
②设△COD的OC边上的高为h，当t为何值时，h的值最大？

科目： 来源：2016-2017学年广东省东莞市堂星晨学校七年级3月月考数学试卷（解析版） 题型：解答题

科目： 来源： 题型：填空题

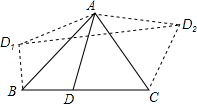3．如图，在△ABC中，∠ABC=45°，∠ACB=60°，BC=2$\sqrt{3}$+2，D是BC边上异于B、C的一动点，将三角形ABD沿AB翻折得到△ABD₁，将△ACD沿AC翻折得到△ACD₂，连接D₁D₂，则四边形D₁BCD₂的面积的最大值是9+4$\sqrt{3}$．