
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:填空题
如图,PA、PB分别切?O于点A、B,若∠P=70°,则∠C的大小为________.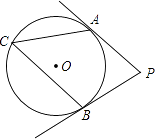
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:填空题
如图,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2,BE=DH=1,点P是直线EF、GH之间任意一点,连接PE、PF、PG、 PH,则∆PEF和∆PGH的面积和等于________.
PH,则∆PEF和∆PGH的面积和等于________.

查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:选择题
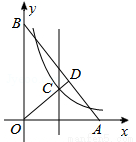
(4分)如图,在直角坐标系xOy中,点A,B分别在x轴和y轴, .∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数
.∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数 的图象过点C.当以CD为边的正方形的面积为
的图象过点C.当以CD为边的正方形的面积为 时,k的值是( )
时,k的值是( )
A.2 B.3 C.5 D.7
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
先化简:  ,然后在-1,0,1,2四个数中选 一个你认为合适的数代入求值.
,然后在-1,0,1,2四个数中选 一个你认为合适的数代入求值.
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
某班13位同学参加每周一次的卫生大扫除,按学校的卫生要求需要完成总面积为60m2的三个项目的任务,三个项目的面积比例和每人每分钟完成各项目的工作量如图所示:
(1)从统计图中可知:擦玻璃的面积占总面积的百分比为________,每人每分钟擦课桌椅________m2;
(2)扫地拖地的面积是________m2;
(3)他们一起完成扫地和拖地任务后,把这13人分成两组,一组去擦玻璃,一组去擦课桌椅,如果你是卫生委员,该如何分配这两组的人数,才能最快地完成任务?(要有详细的解答过程)
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
在∆ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.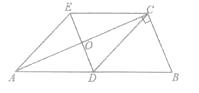
(1)求证:四边形ADCE是菱形;
(2)若AC=2DE,求sin∠CDB的值.
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
甲、乙两个仓库向A、B两地运送水泥,已知甲库可调出100吨水泥,乙库可调出80吨水泥,A地需70吨,B地需110吨水泥,两库到A,B两地的路程和费用如下表:(表中运费“元/吨·千米”表示每吨水泥运送1千米所需要人民币).
路程(千米) | 运费(元/吨·千米) | |||
甲库 | 乙库 | 甲库 | 乙库 | |
A地 | 20 | 15 | 12 | 12 |
B地 | 25 | 20 | 10 | 8 |
设甲库运往A地水泥x吨,总运费W元.
(1)写出w关于x的函数关系式,并求x为何值时总运费最小?
(2)如果要求运送的水泥数是 10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
10吨的整数倍,且运费不能超过38000元,则总共有几种运送方案?
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
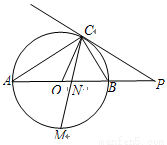
(1)求证:PC是⊙O的切线;
(2)求证:BC=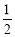 AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN MC的值.
MC的值.
查看答案和解析>>
科目: 来源:【全国区级联考】广东省深圳市罗湖区2017届九年级下学期第二次调研(二模)数学试卷 题型:解答题
如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时 间为t秒,当t为何值时,以P,Q,C为顶点的三角形与∆ADE相似?
间为t秒,当t为何值时,以P,Q,C为顶点的三角形与∆ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com