
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
学校召集留守儿童过端午节,桌上摆有甲、乙两盘粽子,每盘中盛有白粽2个,豆沙粽1个,肉粽1个(粽子外观完全一样).
(1)小明从甲盘中任取一个粽子,取到豆沙粽的概率是 ;
(2)小明在甲盘和乙盘中先后各取了一个粽子,请用树状图或列表法求小明恰好取到两个白粽子的概率.
查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
乌江快铁大桥是快铁渝黔线的一项重要工程,由主桥AB和引桥BC两部分组成(如图所示),建造前工程师用以下方式做了测量;无人机在A处正上方97m处的P点,测得B处的俯角为30°(当时C处被小山体阻挡无法观测),无人机飞行到B处正上方的D处时能看到C处,此时测得C处俯角为80°36′.
(1)求主桥AB的长度;
(2)若两观察点P、D的连线与水平方向的夹角为30°,求引桥BC的长.
(长度均精确到1m,参考数据: ≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)
≈1.73,sin80°36′≈0.987,cos80°36′≈0.163,tan80°36′≈6.06)

查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
贵州省是我国首个大数据综合试验区,大数据在推动经济发展、改善公共服务等方面日益显示出巨大的价值,为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:

(1)本次参与调查的人数有 人;
(2)关注城市医疗信息的有 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是 度;
(4)说一条你从统计图中获取的信息.
查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
如图,PA、PB是⊙O的切线,A、B为切点,∠APB=60°,连接PO并延长与⊙O交于C点,连接AC,BC.
(1)求证:四边形ACBP是菱形;

(2)若⊙O半径为1,求菱形ACBP的面积.
查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
为厉行节能减排,倡导绿色出行,今年3月以来.“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区,某公司拟在甲、乙两个街道社区投放一批“小黄车”,这批自行车包括A、B两种不同款型,请回答下列问题:
问题1:单价
该公司早期在甲街区进行了试点投放,共投放A、B两型自行车各50辆,投放成本共计7500元,其中B型车的成本单价比A型车高10元,A、B两型自行车的单价各是多少?
问题2:投放方式
该公司决定采取如下投放方式:甲街区每1000人投放a辆“小黄车”,乙街区每1000人投放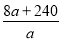 辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
辆“小黄车”,按照这种投放方式,甲街区共投放1500辆,乙街区共投放1200辆,如果两个街区共有15万人,试求a的值.
查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
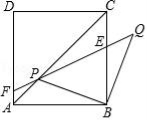
边长为2 的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
的正方形ABCD中,P是对角线AC上的一个动点(点P与A、C不重合),连接BP,将BP绕点B顺时针旋转90°到BQ,连接QP,QP与BC交于点E,QP延长线与AD(或AD延长线)交于点F.
(1)连接CQ,证明:CQ=AP;
(2)设AP=x,CE=y,试写出y关于x的函数关系式,并求当x为何值时,CE= BC;
BC;
(3)猜想PF与EQ的数量关系,并证明你的结论.
查看答案和解析>>
科目: 来源:2017年初中毕业升学考试(贵州遵义卷)数学(解析版) 题型:解答题
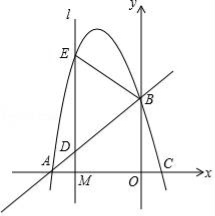
如图,抛物线y=ax2+bx﹣a﹣b(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为y= x+
x+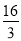 .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
i:探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转, 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
ii:试求出此旋转过程中,(NA+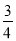 NB)的最小值.
NB)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com