
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
已知关于x的方程 .
.
(1)求证:方程恒有两个不相等的实数根 ;
(2)若此方程的一个根是1,请求出方程的另一个根.
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
某商品现在的售价为每件60元,每星期可卖出300件,市场调查反映:每降价1元,每星期可多卖出20件。已知商品的进价为每件40元,在顾客得到实惠的前提下,商家还想获得6080元的利润,应将销售单价定为多少元?
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
国家射击队将从甲、乙两名运动员中选拔一人参加奥运会比赛,对他们进行了六次测试,测试成绩如下表:(单位:环)
成绩 | 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,计算出甲的平均成绩是 环,乙的平均成绩是 环;
(2)分别计算甲、乙六次测试成绩的方差;
(3)根据(1)、(2)计算的结果,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
王老师获得一张联欢晚会的门票,想奖给班级学校优秀的同学,通过考察,小明和小刚脱颖而出,但问题是只有一张门票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看晚会,他们各自提出了一个方案:
(1)小明的方案:将红桃2、3、4、5四张牌背面朝上,小明先抽一张,记下牌面数字后放回,小刚再从中抽一张,若两张牌上的数字之和是奇数,则小明看晚会,否则小刚看晚会,你认为小明的方案公平吗?请用列表法或画树状图的方法说明;
(2)小刚将小明的方案修改为只用红桃2、3、4三张牌,抽取方式规则不变,小刚的方案公平吗?(只回答,不说明理由)
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
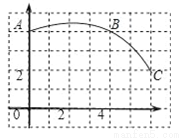
如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:
(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
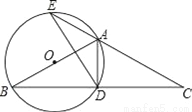
如图,△ABC中,AB=AC,以AB为直径作⊙O,交BC于点D,交CA的延长线于点E,连接AD、DE.
(1)求证:D是BC的中点;
(2)若DE=3,BD﹣AD=2,求⊙O的半径;
(3)在(2)的条件下,求弦AE的长.
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
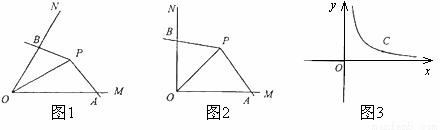
如图1,点P为∠MON的平分线上一点,以P为顶点的角的两边分别与射线OM,ON交于A,B两点,如果∠APB绕点P旋转时始终满足 ,我们就把∠APB叫做∠MON的智慧角.
,我们就把∠APB叫做∠MON的智慧角.
(1)如图2,已知∠MON=90°,点P为∠MON的平分线上一点,以点P为顶点的角的两边分别与射线OM,ON交于A,B两点,且∠APB=135°. 求证:∠APB是∠MON的智慧角;
(2)如图3,C是函数 图象上的一个动点,过点C的直线CD分别交
图象上的一个动点,过点C的直线CD分别交 轴和
轴和 轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
轴于点A,B两点,且满足BC=2CA,请求出∠AOB的智慧角∠APB的顶点P的坐标.
查看答案和解析>>
科目: 来源:江苏省仪征市2017届九年级上学期第二次数学试卷 题型:解答题
阅读资料:小明是一个爱动脑筋的好学生,他在学习了有关圆的切线性质后,意犹未尽,又查阅到了与圆的切线相关的一个问题:
如图1,已知PC是⊙O的切线,AB是⊙O的直径,延长BA交切线PC与P,连接AC、BC、OC.
因为PC是⊙O的切线,AB是⊙O的直径,所以∠OCP=∠ACB=90°,所以∠1=∠2.
又因为∠B=∠1,所以∠B=∠2.
在△PAC与△PCB中,又因为:∠P=∠P,所以△PAC∽△PCB,所以 ,即PC2=PA•PB.
,即PC2=PA•PB.
问题拓展:
(Ⅰ)如果PB不经过⊙O的圆心O(如图2)等式PC2=PA•PB,还成立吗?请证明你的结论;
综合应用:
(Ⅱ)如图3,⊙O是△ABC的外接圆,PC是⊙O的切线,C是切点,BA的延长线交PC于点P;
(1)当AB=PA,且PC=12时,求PA的值;
(2)D是BC的中点,PD交AC于点E.求证: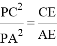 .
.

查看答案和解析>>
科目: 来源:广东省东莞市堂星晨学校2017届九年级上学期12月月考(期末模拟)数学试卷 题型:单选题
用配方法解方程x2﹣2x﹣5=0时,原方程应变形为( )
A. (x+1)2=6 B. (x+2)2=9 C. (x﹣1)2=6 D. (x﹣2)2=9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com