如图，△ABC中BA=BC，点D是AB延长线上一点，DF⊥AC于F交BC于E，

求证：△DBE是等腰三角形．

求证：任意三角形的三个外角中至多有一个直角．

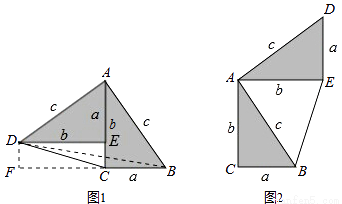
勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：

将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2.

证明：连结DB，过点D作BC边上的高DF，则DF=EC=b﹣a，

∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab．

又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a（b﹣a）

∴ 12 b2+ 12 ab= 12 c2+ 12 a（b﹣a）

∴a2+b2=c2

请参照上述证法，利用图2完成下面的证明．

将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2 ．

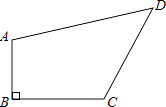
已知：如图，四边形ABCD中，AB⊥BC，AB=1，BC=2，CD=2，AD=3，求四边形ABCD的面积．

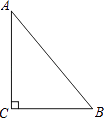
如图是一块直角三角形的绿地，量得直角边BC为6cm，AC为8cm，现在要将原绿地扩充后成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后的等腰三角形绿地的周长．

直角坐标系中，圆心O'的坐标是(2，0)，的半径是4，则点P(－2，1)与⊙O'的位置关系是（ ）

A. 点在圆上 B. 点在圆内 C. 点在圆外 D. 不能确定

如图，在⊙O中，直径CD⊥弦AB，则下列结论中正确的是（ ）

A. AC=AB B. ∠C=∠BOD C. ∠C=∠B D. ∠A=∠BOD

如图，已知AC是⊙O的直径，点B在圆周上(不与A、C重合)，点D在AC的延长线上，连接BD交⊙O于点E，若∠AOB=3∠ADB，则（ ）

A. DE=EB B. DE=EB C. DE=DO D. DE=OB

如图所示，直线AB， AD与⊙O分别相切于点B， D， C为⊙O上一点，且∠BCD=140°，则∠A的度数是（ ）

A. 70° B. 105° C. 100° D. 110°

如图，AP为⊙O的切线，P为切点，若∠A=20°，C、D为圆周上的两点，且∠PDC=60°，则∠OBC等于（ ）

A. 55° B. 65° C. 70° D. 75°