
科目: 来源: 题型:
【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
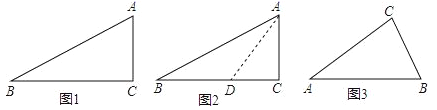
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
查看答案和解析>>
科目: 来源: 题型:
【题目】在正方形ABCD中,DE为正方形的外角∠ADF的角平分线,点G在线段AD上,过点G作PG⊥DE于点P,连接CP,过点D作DQ⊥PC于点Q,交射线PG于点H.
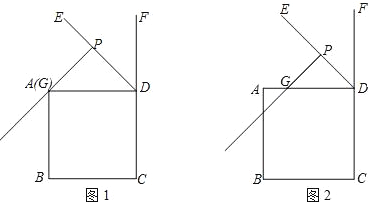
(1)如图1,若点G与点A重合.
①依题意补全图1;
②判断DH与PC的数量关系并加以证明;
(2)如图2,若点H恰好在线段AB上,正方形ABCD的边长为1,请写出求DP长的思路(可以不写出计算结果).
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知点(1,3)在函数y=![]() 的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=
的图象上,矩形ABCD的边BC在x轴正半轴上,E是对角线BD的中点,函数y=![]() (x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
(x>0)的图象又经过A、E两点,点E的横坐标为m,解答下列问题:
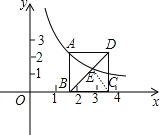
(1)求k的值;
(2)求点C的横坐标(用m表示);
(3)当∠ABD=45°,求m的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】观察下列等式:32-12=8×1;52-32=8×2;72-52=8×3;…,请用含正整数n的等式表示你所发现的规律:___________________.
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
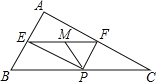
A.1.2 B.1.3 C.1.4 D.2.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com