
科目: 来源: 题型:
【题目】一位“粗心”的同学在做加减运算时,将“-100”错写成“+100”进行运算,这样他得到的结果比正确答案( )
A. 少100 B. 少200 C. 多100 D. 多200
查看答案和解析>>
科目: 来源: 题型:
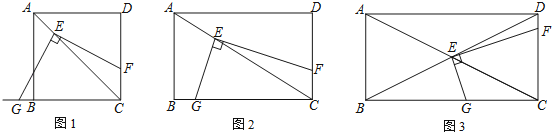
【题目】(1)如图1,将直角的顶点E放在正方形ABCD的对角线AC上,使角的一边交CD于点F,另一边交CB或其延长线于点G,求证:EF=EG;
(2)如图2,将(1)中的“正方形ABCD”改成“矩形ABCD”,其他条件不变.若AB=m,BC=n,试求![]() 的值;
的值;
(3)如图3,将直角顶点E放在矩形ABCD的对角线交点,EF、EG分别交CD与CB于点F、G,且EC平分∠FEG.若AB=2,BC=4,求EG、EF的长.
考点:四边形综合题.
查看答案和解析>>
科目: 来源: 题型:
【题目】为了丰富群众文化生活,某县城区已经整体转换成了数字电视.目前该县广播电视信息网络公司正在对乡镇进行数字电视改装.公司现有400户申请了但还未安装的用户,此外每天还有新的用户申请.已知每个安装小组每天安装的数量相同,且每天申请安装的用户数也相同,公司若安排3个安装小组同时安装,则50天可以安装完所有新、旧申请用户;若公司安排5个安装小组同时安装,则10天可以安装完所有新,旧申请用户.
(1)求每天新申请安装的用户数及每个安装小组每天安装的数量;
(2)如果要求在8天内安装完所有新、旧申请用户,但前3天只能派出2个安装小组安装,那么最后几天至少需要增加多少个安装小组同时安装,才能完成任务?
查看答案和解析>>
科目: 来源: 题型:
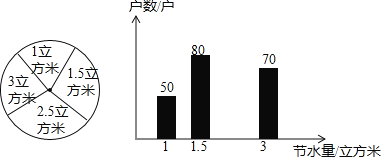
【题目】 “节约用水、人人有责”,某班学生利用课余时间对金辉小区300户居民的用水情况进行了统计,发现5月份各户居民的用水量比4月份有所下降,并且将5月份各户居民的节水量统计整理成如图所示的统计图表
节水量/立方米 | 1 | 1.5 | 2.5 | 3 |
户数/户 | 50 | 80 | a | 70 |
(1)写出统计表中a的值和扇形统计图中2.5立方米对应扇形的圆心角度数.
(2)根据题意,将5月份各居民的节水量的条形统计图补充完整.
(3)求该小区300户居民5月份平均每户节约用水量,若用每立方米水需4元水费,请你估算每户居民1年可节约多少元钱的水费?
查看答案和解析>>
科目: 来源: 题型:
【题目】综合与探究:
如图,抛物线y=![]() x2﹣
x2﹣![]() x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
x﹣4与x轴交与A,B两点(点B在点A的右侧),与y轴交于点C,连接BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l交抛物线于点Q.
(1)求点A,B,C的坐标.
(2)当点P在线段OB上运动时,直线l分别交BD,BC于点M,N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由.
(3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

考点:二次函数综合题.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)如图①,在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF分别交AD、BC于点E、F,
求证:OE=OF.
(2)在图①中,过点O作直线GH分别交AB、CD于点G、H,且满足GH⊥EF,连结EG、GF、FH、HE.如图②,试判断四边形EGFH的形状,并说明理由;
(3)在(2)的条件下,
若平行四边形ABCD变为矩形时,四边形EGFH是 ;
若平行四边形ABCD变为菱形时,四边形EGFH是 ;
若平行四边形ABCD变为正方形时,四边形EGFH是 .
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两人玩摸球游戏,从放有足够多球的箱子中摸球,规定每人最多两种取法,甲每次摸4个或(3-k)个,乙每次摸5个或(5-k)个(k是常数,且0<k<3);经统计,甲共摸了16次,乙共摸了17次,并且乙至少摸了两次5个球,最终两人所摸出的球的总个数恰好相等,那么箱子中至少有球__________个.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com