
科目: 来源: 题型:
【题目】(Ⅰ)(1)问题引入
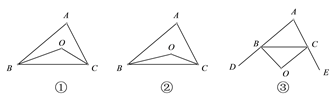
如图①,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
(2)拓展研究
如图②,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,试求∠BOC的度数 (用α表示).(3)归纳猜想
∠ACB,∠A=α,试求∠BOC的度数 (用α表示).(3)归纳猜想
若BO、CO分别是△ABC的∠ABC、∠ACB的n等分线,它们交于点O,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示).
∠ACB,∠A=α,则∠BOC= (用α表示).
(Ⅱ)类比探索
(1)特例思考
如图③,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,求∠BOC的度数(用α表示).
∠ECB,∠A=α,求∠BOC的度数(用α表示).
(2)一般猜想
若BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= (用α表示).
∠ECB,∠A=α,请猜想∠BOC= (用α表示).
查看答案和解析>>
科目: 来源: 题型:
【题目】证明定理:三角形三条边的垂直平分线相交于一点,并且这一点到三个顶点的距离相等,已知:
如图,在△ABC中,分别作AB边、BC边的垂直平分线,两线相交于点P,分别交AB边、BC边于点E、F.
求证:AB、BC、AC的垂直平分线相交于点P
证明:∵点P是AB边垂直平线上的一点,
∴ = ( ).
同理可得,PB= .
∴ = (等量代换).
∴ (到一条线段两个端点距离相等的点,在这条线段的 )
∴AB、BC、AC的垂直平分线 .
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=-x2-2x+3 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
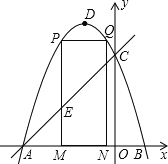
(1)求A、B、C的坐标;
(2)设点H是第二象限内抛物线上的一点,且△HAB的面积是6,求点H的坐标;
(3)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com