
科目: 来源: 题型:
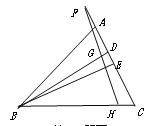
【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,某校要用20m的篱笆,一面靠墙(墙长10m),围成一个矩形花圃,设矩形花圃垂直于墙的一边长为xm,花圃的面积为ym2.

(1)求出y与x的函数关系式.
(2)当矩形花圃的面积为48m2时,求x的值.
(3)当边长x为多少时,矩形的面积最大,最大面积是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90,则∠BCE 度;
(2)设∠BAC=,∠BCE=.
①如图2,当点D在线段BC上移动,则,之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则,之间有怎样的数量关系?请直接写出你的结论,不必说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知抛物线y=x2﹣2mx﹣4(m>0)的顶点M关于坐标原点O的对称点为M′,若点M′在这条抛物线上,则点M的坐标为( )
A.(1,﹣5)
B.(3,﹣13)
C.(2,﹣8)
D.(4,﹣20)
查看答案和解析>>
科目: 来源: 题型:
【题目】【阅读理解】对于任意正实数a、b,
∵(![]() -
-![]() )2≥0,∴a-2
)2≥0,∴a-2![]() +b≥0,
+b≥0,
∴a+b≥2![]() ,(只有当a=b时,a+b等于2
,(只有当a=b时,a+b等于2![]() ).
).
【获得结论】在a+b≥2![]() (a、b均为正实数)中,若ab为定值p,
(a、b均为正实数)中,若ab为定值p,
则a+b≥2![]() ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2![]() .
.
根据上述内容,回答下列问题:(1)若![]() >0,只有当
>0,只有当![]() = 时,m+
= 时,m+![]() 有最小值 .
有最小值 .
【探索应用】(2)已知点Q(-3,-4)是双曲线y=![]() 上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=
上一点,过Q作QA⊥x轴于点A,作QB⊥y轴于点B.点P为双曲线y=![]() (x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.
(x>0)上任意一点,连接PA,PB,求四边形AQBP的面积的最小值.

查看答案和解析>>
科目: 来源: 题型:
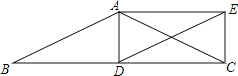
【题目】如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目: 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:
不成立,但有些数可以使得它成立,例如: ![]() .我们称使得
.我们称使得![]() 成立的一对数
成立的一对数![]() 为“相伴数对”,记为(
为“相伴数对”,记为(![]() ).
).
(1)若(![]() )是“相伴数对”,求b的值;
)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”( ![]() ),其中
),其中![]() 且
且![]() ;
;
(3)若(![]() )是“相伴数对”,求代数式
)是“相伴数对”,求代数式![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com