【题目】把多边形的某些边向两方延长，其他各边若不全在延长所得直线的同侧，则把这样的多边形叫做凹多边形.如图①五边形中，作直线,则边、分别在直线的两侧，所以五边形就是一个凹五边形.我们简单研究凹多边形的边和角的性质.

（1）如图②,在凹六边形中，探索与、、、、、之间的关系；

（2）如图③,在凹四边形中，证明．

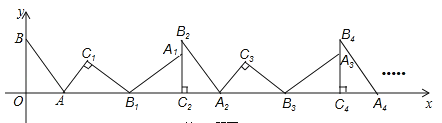
【题目】如图，在平面直角坐标系中，将△ABO绕点A顺时针旋转到△AB1C1的位置，点B、O分别落在点B1、C1处，点B1在x轴上，再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置，点C2在x轴上，将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置，点A2在x轴上，依次进行下去…．若点A（，0），B（0，2），则点B2016的坐标为______________．

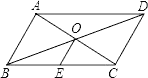
A. OE=DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE

我们知道的几何意义是在数轴上数对应的点与原点的距离： ，也就是说， 表示在数轴上数与数0对应点之间的距离；

这个结论可以推广为表示在数轴上数和数对应的点之间的距离；

例1解方程，容易看出，在数轴上与原点距离为2的点对应的数为，即该方程的解为．

例2解不等式，如图，在数轴上找出的解，即到1的距离为2的点对应的数为，3，则的解集为或.

例3解方程由绝对值的几何意义知，该方程表示求在数轴上与1和的距离之和为5的对应的的值.在数轴上，1和的距离为3，满足方程的对应的点在1的右边或的左边，若对应的点在1的右边，由下图可以看出；同理，若对应的点在的左边，可得，故原方程的解是或.

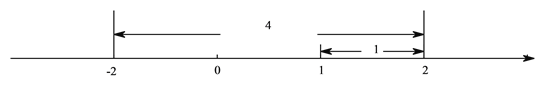
回答问题：（只需直接写出答案）

①解方程

②解不等式

③解方程

（1）本次调查的八年级部分学生共有______名；请补全条形统计图；

（2）若该校八年级学生共有540人，请你估计该校八年级有多少名学生支持“分组合作学习”方式（含“非常喜欢”和“喜欢”两种情况的学生）？

【题目】如图，、、分别平分的外角、内角、外角．以下结论：①：②：③：④．其中正确的结论有（ ）

A. 1个 B. 2个 C. 3个 D. 4个

【题目】某部队将在指定山区进行军事演习，为了使道路便于部队重型车辆通过，部队工兵连接到抢修一段长3600米道路的任务，按原计划完成总任务的后，为了让道路尽快投入使用，工兵连将工作效率提高了50%，一共用了10小时完成任务．

（1）按原计划完成总任务的时，已抢修道路　 　米；

（2）求原计划每小时抢修道路多少米？

【题目】如图（1），点为线段上一点，过点作射线，使，将一直角三角板的直角顶点放在点处，一边在射线上，另一边在线段的下方.

（1）将图（1）中的直角三角板绕点按逆时针方向旋转，使落在射线上（如图（2）），则三角板旋转的角度为____度；

（2）继续将图2中的直角三角板绕点按逆时针方向旋转，使在的内部（如图3）.试求与度数的差；

（3）若图1中的直角三角板绕点按逆时针方向旋转一周，在此过程中：

①当直角边所在直线恰好垂直于时， 的度数是________；

②设直角三角板绕点按每秒的速度旋转，当直角边所在直线恰好平分时，求三角板绕点旋转时间的值.

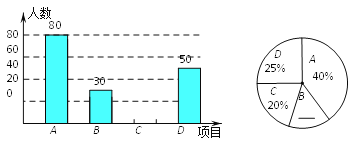
（1）本次共调查了多少名学生？

（2）请将两个统计图补充完整.

（3）若该中学有1200名学生，喜欢篮球运动项目的学生约有多少名？

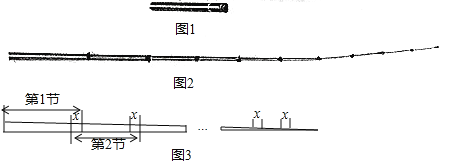
（1）请直接写出第5节套管的长度；

（2）当这根鱼竿完全拉伸时，其长度为311cm，求x的值．