
科目: 来源: 题型:
【题目】阅读下面材料:
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
![]()
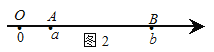
当A、B两点都不在原点时,如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
如图3,当点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;
=∣a-b∣;
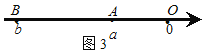
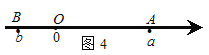
如图4,当点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= ![]() =∣a-b∣;
=∣a-b∣;
回答下列问题:
(1)数轴上表示1和6的两点之间的距离是 ,数轴上表示2和-3的两点之间的距离是 ;
(2)数轴上若点A表示的数是x,点B表示的数是-4,则点A和B之间的距离是 ,若∣AB∣=3,那么x为 ;
(3)当x是 时,代数式![]() ;
;
(4)若点A表示的数![]() ,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒
,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
个单位长度,求运动几秒后,点Q与点P 相距1个单位?(请写出必要的求解过程)
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在□ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:△ADE≌△CBF;
(2)当AD⊥BD时,请你判断四边形BFDE的形状,并说明理由.

查看答案和解析>>
科目: 来源: 题型:
【题目】商场销售某种冰箱,该种冰箱每台进价为2500元.已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了x元.
(1)填表(不需化简):
每天的销售量/台 | 每台销售利润/元 | |
降价前 | 8 | 400 |
降价后 |
(2)商场为使这种冰箱平均每天的销售利润达到5000元,则每台冰箱的实际售价应定为多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,![]() ,设c为最长边.当
,设c为最长边.当![]() 时,△ABC是直角三角形;当
时,△ABC是直角三角形;当![]() 时,利用代数式
时,利用代数式![]() 和
和![]() 的大小关系,可以判断△ABC的形状(按角分类).
的大小关系,可以判断△ABC的形状(按角分类).
(1)请你通过画图探究并判断:当△ABC三边长分别为6,8,9时,△ABC为____三角形;当△ABC三边长分别为6,8,11时,△ABC为______三角形.
(2)小明同学根据上述探究,有下面的猜想:“当![]() 时,△ABC为锐角三角形;当
时,△ABC为锐角三角形;当![]() 时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
时,△ABC为钝角三角形.”请你根据小明的猜想完成下面的问题:
当![]() ,
,![]() 时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?
查看答案和解析>>
科目: 来源: 题型:
【题目】已知点![]() 为某封闭图形边界上一定点,动点
为某封闭图形边界上一定点,动点![]() 从点
从点![]() 出发,沿其边界顺时针匀速运动一周.设点
出发,沿其边界顺时针匀速运动一周.设点![]() 运动的时间为
运动的时间为![]() ,线段
,线段![]() 的长为
的长为![]() .表示
.表示![]() 与
与![]() 的函数关系的图象大致如右图所示,则该封闭图形可能是( )
的函数关系的图象大致如右图所示,则该封闭图形可能是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com