练习册

  • 练习册
  • 试题
    相关习题
     0  339305  339313  339319  339323  339329  339331  339335  339341  339343  339349  339355  339359  339361  339365  339371  339373  339379  339383  339385  339389  339391  339395  339397  339399  339400  339401  339403  339404  339405  339407  339409  339413  339415  339419  339421  339425  339431  339433  339439  339443  339445  339449  339455  339461  339463  339469  339473  339475  339481  339485  339491  339499  366461 

    科目： 来源： 题型：

    【题目】近似数2.40×104精确到________位.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】（12分）在等腰△ABC中，AB=AC=2, ∠BAC=120°,AD⊥BC于D,点O、点P分别在射线AD、BA上的运动，且保证∠OCP=60°，连接OP.

    （1）当点O运动到D点时，如图一，此时AP=______,△OPC是什么三角形。

    （2）当点O在射线AD其它地方运动时，△OPC还满足（1）的结论吗？请用利用图二说明理由。

    （3）令AO=x，AP=y，请直接写出y关于x的函数表达式，以及x的取值范围。

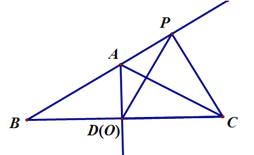
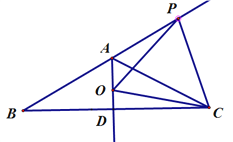
    图一 图二

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】为了进行资源的再利用，学校准备针对库存的桌椅进行维修，现有甲、乙两木工组，甲每天修桌凳14 套，乙每天比甲多7套，甲单独修完这些桌凳比乙单独修完多用20天．学校每天付甲组80元修理费，付乙组120元修理费．

    （1）请问学校库存多少套桌凳?

    （2）在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案：①由甲单独修理；②由乙单独修理；③甲、乙合作同时修理．你选哪种方案，为什么?

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】某同学做数学题：已知两个多项式A、B，其中B＝4x2―3x＋7，他在求A＋B时，把A＋B错看成了A―B，求得的结果为8x2＋x＋1.请你帮助这位同学求出A＋B的正确结果.

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数（单位：cm）与方差，要从中选择一名成绩好又发挥稳定的运动员参加决赛，最合适的是（　　）

    甲

    乙

    丙

    丁

    平均数

    610

    585

    610

    585

    方差

    12.5

    13.5

    2.4

    5.4

    A.甲B.乙C.丙D.丁

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】下面的计算正确的是（ ）
    A.6a﹣5a=1
    B.a+2a2=3a3
    C.﹣（a﹣b）=﹣a+b
    D.2（a+b）=2a+b

    查看答案和解析>>

    科目： 来源： 题型：

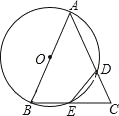
    【题目】(2016宁夏第23题)已知△ABC，以AB为直径的⊙O分别交AC于D，BC于E，连接ED，若ED=EC．

    （1）求证：AB=AC；

    （2）若AB=4，BC=2，求CD的长．

    查看答案和解析>>

    科目： 来源： 题型：

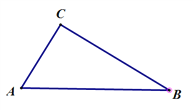
    【题目】（8分）如图，在Rt△ABC中，∠ACB=Rt∠。

    （1）请用直尺和圆规，过点C作AB边上的高线，交AB于D,作∠B的角平分线，交AC于E，交CD与F。

    （2）△CEF是什么三角形，请说明理由

    查看答案和解析>>

    科目： 来源： 题型：

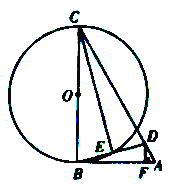
    【题目】(2016贵州省毕节市第26题)如图，在△ABC中，D为AC上一点，且CD=CB,以BC为直径作☉O,交BD于点E，连接CE,过D作DFAB于点F,∠BCD=2∠ABD.

    (1)、求证：AB是☉O的切线；(2)、若∠A=60°，DF=,求☉O的直径BC的长。

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在平行四边形ABCD中，∠A的平分线交DC于E，若∠DEA＝30°，则∠B＝（ ）．
    A.100°
    B.120°
    C.135°
    D.150°

    查看答案和解析>>

    同步练习册答案