
科目: 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪灵感.他惊喜地发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连接DB,过点D作BC边上的高DF,则DF=EC=b-a.
∵S四边形ADCB=S△ACD+S△ABC=![]() b2+
b2+![]() ab.
ab.
又∵S四边形ADCB=S△ADB+S△DCB=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴![]() b2+
b2+![]() ab=
ab=![]() c2+
c2+![]() a(b-a),
a(b-a),
∴a2+b2=c2.
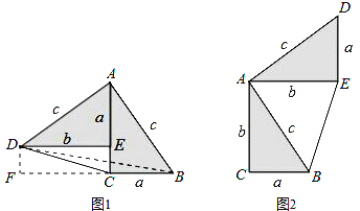
请参照上述证法,利用图2完成下面的证明:
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
证明:连接 ,
∵S五边形ACBED= ,
又∵S五边形ACBED= ,
∴ ,
∴a2+b2=c2.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1)化简:5m2-7n-8mn+5n-9m2+8mn.
(2)已知:a-2b=4,ab=1.试求代数式(-a+3b+5ab)-(5b-2a+6ab)的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】某家电生产企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、冰箱、彩电共360台,且彩电至少生产60台,已知生产这些家电产品每台所需工时和每台产值如下表:
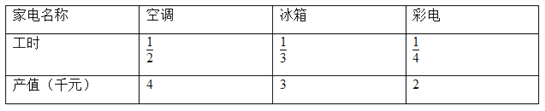
问每周应生产空调、冰箱、彩电各多少台,才能使产值最高?最高产值是多少?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了弘扬“中国梦”,某校初三(1)班和(2)班各5名学生参加以“诚信友善”为主题的演讲比赛活动,根据他们的得分情况绘制如下的统计图:
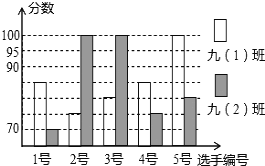
(1)求初三(1)班5名同学得分的平均数和初三(2)班5名同学得分的众数;
(2)你认为哪个班5名同学参赛的整体成绩要好些?为什么?
(3)如果在每班参加复赛的选手中分别选出2人参加决赛,你认为哪个班的实力更强一些,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com