
科目: 来源: 题型:
【题目】甲、乙、丙、丁四人进行100m短跑训练,统计近期10次测试的平均成绩都是13.2s,10次测试成绩的方差如下表则这四人中发挥最稳定的是( )
选手 | 甲 | 乙 | 丙 | 丁 |
方差(s2) | 0.020 | 0.019 | 0.021 | 0.022 |
A.甲B.乙C.丙D.丁
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解某市水稻的亩产量,随机抽取六块试验田进行调查,它们的亩产量分别为(单位:斤):1000,1100,
1250,1050,1100,1200,则这组数据的众数为斤.
查看答案和解析>>
科目: 来源: 题型:
【题目】(1) 定义:直角三角形两直角边的平方和等于斜边的平方.如:直角三角形的直角边分别为3、4,则斜边的平方=32+42=25.已知:Rt△ABC中,∠C=90°,AC=8,AB=10,直接写出BC2=__________________.
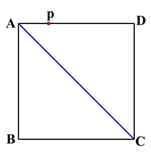
(2)应用:已知正方形ABCD的边长为4,点P为AD边上的一点,AP= ![]() ,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.
,请利用“两点之间线段最短”这一原理,在线段AC上画出一点M,使MP+MD最小,并直接写出最小值的平方为_____________.

查看答案和解析>>
科目: 来源: 题型:
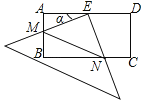
【题目】在矩形ABCD中,AD=2AB=4,E是AD的中点,一块足够大的三角板的直角顶点与点E重合,将三角板绕点E旋转,三角板的两直角边分别交AB,BC(或它们的延长线)于点M,N,设∠AEM=α(0°<α<90°),给出下列四个结论:
①AM=CN;②∠AME=∠BNE;③BN﹣AM=2;④S△EMN=![]() .
.
上述结论中正确的个数是( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目: 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目: 来源: 题型:
【题目】如图在△AFD和△CEB中,点A、E、F、C在同一条直线上.有下面四个论断:
(1)AD=CB,(2)AE=CF,(3)∠B=∠D,(4)AD∥BC.
请用其中三个作为条件,余下一个作为结论,进行证明.

查看答案和解析>>
科目: 来源: 题型:
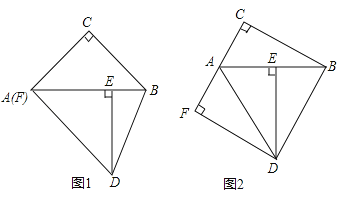
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
(1)如图1,若点F与点A重合,求证:AC=BC;
(2)若∠DAF=∠DBA,①如图2,当点F在线段CA的延长线上时,判断线段AF与线段BE的数量关系,并说明理由;
②当点F在线段CA上时,设BE=x,请用含x的代数式表示线段AF.
查看答案和解析>>
科目: 来源: 题型:
【题目】在某校“我的中国梦”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( ).
A.众数
B.方差
C.平均数
D.中位数
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,面积为6的平行四边形纸片ABCD中,AB=3,∠BAD=45°,按下列步骤进行裁剪和拼图.
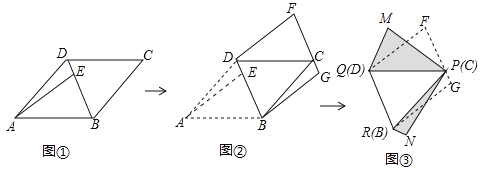
第一步:如图①,将平行四边形纸片沿对角线BD剪开,得到△ABD和△BCD纸片,再将△ABD纸片沿AE剪开(E为BD上任意一点),得到△ABE和△ADE纸片;
第二步:如图②,将△ABE纸片平移至△DCF处,将△ADE纸片平移至△BCG处;
第三步:如图③,将△DCF纸片翻转过来使其背面朝上置于△PQM处(边PQ与DC重合,△PQM和△DCF在DC同侧),将△BCG纸片翻转过来使其背面朝上置于△PRN处,(边PR与BC重合,△PRN和△BCG在BC同侧).则由纸片拼成的五边形PMQRN中,对角线MN长度的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com