【题目】在平面直角坐标系中，点P（2，﹣3）在（　　）
A.第一象限
B.第二象限
C.第三象限
D.第四象限

（1）线段BE的长；

（2）∠ECB的余切值．

【题目】3x2可以表示为（ ）
A.x2+x2+x2
B.x2x2x2
C.3x3x
D.9x

【题目】某国发生8.1级强烈地震，我国积极组织抢险队赴地震灾区参与抢险工作，如图，某探测对在地面A、B两处均探测出建筑物下方C处由生命迹象，已知探测线与地面的夹角分别是25°和60°，且AB=4米，求该生命迹象所在位置C的深度．（结果精确到1米，参考数据：sin25°≈0.4，cos25°≈0，9，tan25°≈0.5，≈1.7）

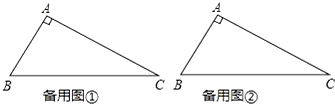
（1）已知△ABC中，∠A=90°，∠B=67.5°，请画一条直线，把这个三角形分割成两个等腰三角形．（请你选用下面给出的备用图，并把所有不同的分割方法都画出来，图不够可以自己画．只需画图，不必说明理由，但要在图中标出相等两角的度数）．

（2）已知等腰△ABC中，AB=AC，D为BC上一点，连接AD，若△ABD和△ACD都是等腰三角形，则∠B的度数为　　（请画出示意图，并标明必要的角度）．

A.40°B.50°C.130°D.150°

【题目】（2016江西省）设抛物线的解析式为 ，过点B1 （1，0 ）作x轴的垂线，交抛物线于点A1（1，2 ）；过点B2 （1，0 ）作x轴的垂线，交抛物线于点A2 ，… ；过点 （，0 ） （n为正整数 ）作x轴的垂线，交抛物线于点 ，连接 ，得直角三角形．

（1）求a的值；

（2）直接写出线段 ，的长（用含n的式子表示）；

（3）在系列Rt△ 中，探究下列问题：

①当n为何值时，Rt△是等腰直角三角形？

②设1≤k＜m≤n （k，m均为正整数），问是否存在Rt△与Rt△相似？若存在，求出其相似比；若不存在，说明理由．

【题目】如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26，≈1.73）．

A.(9，4)B.(1，2)C.(2，9)D.(5，3)