
科目: 来源: 题型:
【题目】电影《我和我的祖国》讲述了普通人与国家之间息息相关密不可分的动人故事,一上映就获得全国人民的追捧,第一天票房约4亿元,如果以后每天票房按相同的增长率增长,三天后累计票房收入可达12亿元,若增长率记作x,则方程可以列为__________.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,点O是弹力墙MN上一点,魔法棒从OM的位置开始绕点O向ON的位置顺时针旋转,当转到ON位置时,则从ON位置弹回,继续向OM位置旋转;当转到OM位置时,再从OM的位置弹回,继续转向ON位置,…,如此反复.按照这种方式将魔法棒进行如下步骤的旋转:第1步,从OA0(OA0在OM上)开始旋转α至OA1;第2步,从OA1开始继续旋转2α至OA2;第3步,从OA2开始继续旋转3α至OA3 , ….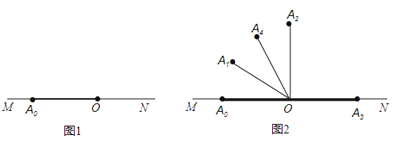
例如:当α=30°时,OA1 , OA2 , OA3 , OA4的位置如图2所示,其中OA3恰好落在ON上,∠A3OA4=120°;
当α=20°时,OA1 , OA2 , OA3 , OA4 , OA3的位置如图3所示,
其中第4步旋转到ON后弹回,即∠A3ON+∠NOA4=80°,而OA3恰好与OA2重合.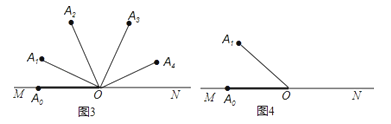
![]()
(1)若α=35°,在图4中借助量角器画出OA2 , OA3 , 其中∠A3OA2的度数是 ;
(2)若α<30°,且OA4所在的射线平分∠A2OA3 , 在如图5中画出OA1 , OA2 , OA3 , OA4并求出α的值
(3)若α<36°,且∠A2OA4=20°,则对应的α值是
(4)当OAi所在的射线是∠AiOAk(i,j,k是正整数,且OAj与OAk不重合)的平分线时,旋转停止,请探究:试问对于任意角α(α的度数为正整数,且α=180°),旋转是否可以停止?写出你的探究思路.
查看答案和解析>>
科目: 来源: 题型:
【题目】一般情况下![]() 不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得
不成立,但有些数可以使得它成立,例如:a=b=0.我们称使得![]() 成立的一对数a,b为“相伴数对”,记为(a,b).
成立的一对数a,b为“相伴数对”,记为(a,b).
(1)若(1,b)是“相伴数对”,求b的值;
(2)写出一个“相伴数对”(a,b),其中a≠0,且a≠1;
(3)若(m,n)是“相伴数对”,求代数式m﹣![]() n﹣[4m﹣2(3n﹣1)]的值.
n﹣[4m﹣2(3n﹣1)]的值.
查看答案和解析>>
科目: 来源: 题型:
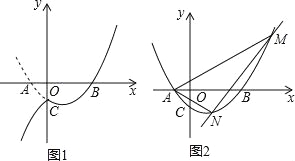
【题目】已知抛物线y=(m﹣1)x2+(m﹣2)x﹣1与x轴交于A、B两点,若m>1,且点A在点B的左侧,OA:OB=1:3
(1)试确定抛物线的解析式;
(2)直线y=kx﹣3与抛物线交于M、N两点,若△AMN的内心在x轴上,求k的值.
(3)设(2)中抛物线与y轴的交点为C,过点C作直线l∥x轴,将抛物线在y轴左侧的部分沿直线l翻折,抛物线的其余部分保持不变,得到一个新图象,请你结合新图象回答:当直线y=![]() x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
x+b与新图象只有一个公共点P(x0,y0)且y0≤7时,求b的取值范围.
查看答案和解析>>
科目: 来源: 题型:
【题目】列方程解应用题:
为了丰富社会实践活动,引导学生科学探究,学校组织七年级同学走进中国科技馆,亲近科学,感受科技魅力.来到科技馆大厅,同学们就被大厅里会“跳舞”的“小球矩阵”吸引住了(如图1).白色小球全部由计算机精准控制,每一只小球可以“悬浮”在大厅上空的不同位置,演绎着曲线、曲面、平面、文字和三维图案等各种动态造型.
已知每个小球分别由独立的电机控制.图2,图3分别是9个小球可构成的两个造型,在每个造型中,相邻小球的高度差均为a.为了使小球从造型一(如图2)变到造型二(如图3),控制电机使造型一中的②,③,④,⑥,⑦,⑧号小球同时运动,②,③,④号小球向下运动,运动速度均为3米/秒;⑥,⑦,⑧号小球向上运动,运动速度均为2米/秒,当每个小球到达造型二的相应位置时就停止运动.已知⑦号小球比②号小球晚![]() 秒到达相应位置,问②号小球运动了多少米?
秒到达相应位置,问②号小球运动了多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com