
科目: 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4个小长方形,然后按图2的形状拼成一个正方形.
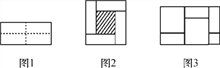
(1)图2中阴影部分的面积为 ;
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,则x-y= ;
(4)实际上有许多恒等式可以用图形的面积来表示,如图3,它表示等式: .
查看答案和解析>>
科目: 来源: 题型:
【题目】计算:
(1)﹣9+(+ ![]() )﹣(﹣12)+(﹣5)+(﹣
)﹣(﹣12)+(﹣5)+(﹣ ![]() )
)
(2)(1﹣1 ![]() ﹣
﹣ ![]() +
+ ![]() )×(﹣24)
)×(﹣24)
(3)﹣ ![]() +
+ ![]() ÷(﹣2)×(﹣
÷(﹣2)×(﹣ ![]() )
)
(4)﹣14﹣(1﹣ ![]() )÷3×|3﹣(﹣3)2|
)÷3×|3﹣(﹣3)2|
查看答案和解析>>
科目: 来源: 题型:
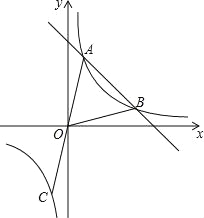
【题目】如图,直线y=﹣x+b与反比例函数![]() 的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
的图象相交于A(1,4),B两点,延长AO交反比例函数图象于点C,连接OB.
(1)求k和b的值;
(2)直接写出一次函数值小于反比例函数值的自变量x的取值范围;
(3)在y轴上是否存在一点P,使![]() ?若存在请求出点P坐标,若不存在请说明理由.
?若存在请求出点P坐标,若不存在请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】问题引入:
(1)如图1,在△ABC中,点O是∠ABC和∠ACB平分线的交点,若∠A=α,则∠BOC= (用α表示);
如图2,∠CBO=![]() ∠ABC,∠BCO=
∠ABC,∠BCO=![]() ∠ACB,∠A=α,则∠BOC= (用α表示);
∠ACB,∠A=α,则∠BOC= (用α表示);
拓展研究:
(2)如图3,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
∠ECB,∠A=α,猜想∠BOC= (用α表示),并说明理由;
(3)BO、CO分别是△ABC的外角∠DBC、∠ECB的n等分线,它们交于点O,∠CBO=![]() ∠DBC,∠BCO=
∠DBC,∠BCO=![]() ∠ECB,∠A=α,请猜想∠BOC= .
∠ECB,∠A=α,请猜想∠BOC= .

查看答案和解析>>
科目: 来源: 题型:
【题目】在数轴上,已知在纸面上有一数轴(如图),折叠纸面. ![]()
(1)若1表示的点与﹣1表示的点重合,则﹣2表示的点与数表示的点重合;
(2)若﹣1表示的点与3表示的点重合,5表示的点与数表示的点重合;
(3)若数轴上A、B两点之间的距离为c个单位长度,点A表示的有理数是a,并且A、B两点经折叠后重合,请写出此时折线与数轴的交点表示的有理数是多少?
查看答案和解析>>
科目: 来源: 题型:
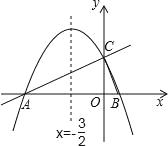
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣
x+2与x轴交于点A,与y轴交于点C.抛物线y=ax2+bx+c的对称轴是x=﹣![]() 且经过A、C两点,与x轴的另一交点为点B.
且经过A、C两点,与x轴的另一交点为点B.
(1)①直接写出点B的坐标;②求抛物线解析式.
(2)若点P为直线AC上方的抛物线上的一点,连接PA,PC.求△PAC的面积的最大值,并求出此时点P的坐标.
(3)抛物线上是否存在点M,过点M作MN垂直x轴于点N,使得以点A、M、N为顶点的三角形与△ABC相似?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】徐老师给爱好学习的小敏和小捷提出这样一个问题:如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC
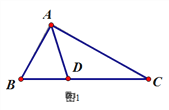
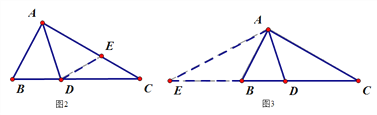
小敏的证明思路是:在AC上截取AE=AB,连接DE.(如图2)
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)请你任意选择一种思路继续完成下一步的证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com