
科目: 来源: 题型:
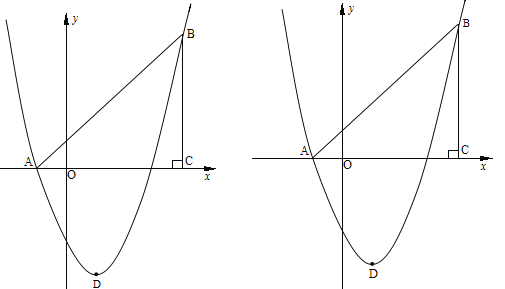
【题目】如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90,AC=BC,OA=1,OC=4,抛物线y=![]() +bx+c经过A,B两点,抛物线的顶点为D.
+bx+c经过A,B两点,抛物线的顶点为D.
(1)、求b,c的值;
(2)、点E是直角三角形ABC斜边AB上一动点(点A、B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)、在(2)的条件下:①求以点E、B、F、D为顶点的四边形的面积;②在抛物线上是否存在一点P,使△EFP是以EF为直角边的直角三角形? 若存在,求出所有点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目: 来源: 题型:
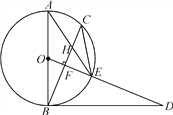
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
求证:(1)BD是⊙O的切线;
(2)若EH=2,AH=6,求CE的长.
查看答案和解析>>
科目: 来源: 题型:
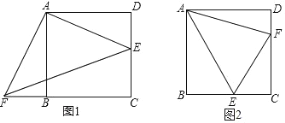
【题目】如图1,四边形ABCD是正方形,△ADE经旋转后与△ABF重合.
(1)旋转中心是 ;旋转角是 度; 如果连接EF,那么△AEF是 三角形.
(2)用上述思想或其他方法证明:如图2,在正方形ABCD中,点E、F分别在BC、CD上,且∠EAF=45°.
求证:EF=BE+DF.
(3)若DF=4,EF=10,求四边形AECD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com