
科目: 来源: 题型:
【题目】如图,∠A=∠B=90°,E是AB上的一点,且AE=BC,∠1=∠2. 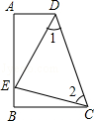
(1)求证:Rt△ADE与Rt△BEC全等;
(2)求证:△CDE是直角三角形.
查看答案和解析>>
科目: 来源: 题型:
【题目】计算
(1)(﹣4x2y3)(﹣ ![]() xyz)÷(
xyz)÷( ![]() xy2)2
xy2)2
(2)(54x2y﹣108xy2﹣36xy)÷(18xy)
(3)(a+b+3)(a+b﹣3)
(4)20070+2﹣2﹣( ![]() )2+2014.
)2+2014.
查看答案和解析>>
科目: 来源: 题型:
【题目】某公司2012年缴税70万元,2014年缴税90万元,求该公司这两年缴税的年平均增长率.若设该公司这两年缴税的年平均增长率为x,根据题意,可得方程( )
A.70x2=90
B.70(1+x)2=90
C.70(1+x)=90
D.70+70(1+x)+70(1+x)2=90
查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于A、B(A点在B点的左侧)与
轴交于A、B(A点在B点的左侧)与![]() 轴交于点C.
轴交于点C.
(1)如图1,连接AC、BC,若△ABC的面积为3时,求抛物线的解析式;
(2)如图2,点P为第四象限抛物线上一点,连接PC,若![]() 时,求点P的横坐标;
时,求点P的横坐标;
(3)如图3,在(2)的条件下,点F在AP上,过点P作PH⊥![]() 轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=
轴于H点,点K在PH的延长线上,AK=KF,∠KAH=∠FKH,PF=![]() ,连接KB并延长交抛物线于点Q,求PQ的长.
,连接KB并延长交抛物线于点Q,求PQ的长.

查看答案和解析>>
科目: 来源: 题型:
【题目】已知:如图,AB∥CD,∠A=∠D,试说明 AC∥DE 成立的理由.
(下面是彬彬同学进行的推理,请你将彬彬同学的推理过程补充完整.)
解:∵AB∥CD (已知)
∴∠A=(两直线平行,内错角相等)
又∵∠A=∠D()
∴∠=∠(等量代换)
∴AC∥DE ()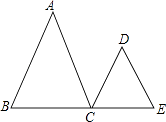
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,BC∥OA,∠B=∠A=100°,试回答下列问题: 
(1)如图①,求证:OB∥AC.
(2)如图②,若点E、F在线段BC上,且满足∠FOC=∠AOC,并且OE平分∠BOF.则∠EOC的度数等于;(在横线上填上答案即可).
(3)在(2)的条件下,若平行移动AC,如图③,那么∠OCB:∠OFB的值是否随之发生变化?若变化,试说明理由;若不变,求出这个比值.
(4)在(3)的条件下,如果平行移动AC的过程中,若使∠OEB=∠OCA,此时∠OCA度数等于 . (在横线上填上答案即可).
查看答案和解析>>
科目: 来源: 题型:
【题目】根据图中给出的信息,解答下列问题: 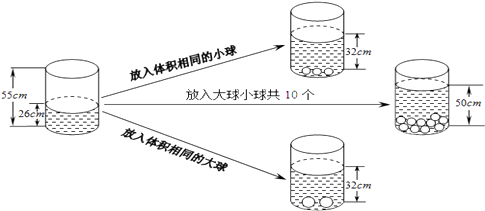
(1)放入一个小球水面升高cm,放入一个大球水面升高cm;
(2)如果要使水面上升到50cm,应放入大球、小球各多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com