
科目: 来源: 题型:
【题目】若直线y=kx+k﹣1经过点(m,n+3)和(m+1,2n﹣1),且0<k<2,则n的取值范围是( )
A. 0<n<2B. 0<n<4C. 2<n<6D. 4<n<6
查看答案和解析>>
科目: 来源: 题型:
【题目】某校为开展好大课间活动,欲购买单价为20元的排球和单价为80元的篮球共100个.
(1)设购买排球数为x(个),购买两种球的总费用为y(元),请你写出y与x的函数关系式(不要求写出自变量的取值范围);
(2)如果购买两种球的总费用不超过6620元,并且篮球数不少于排球数的3倍,那么有哪几种购买方案?
(3)从节约开支的角度来看,你认为采用哪种方案更合算?
查看答案和解析>>
科目: 来源: 题型:
【题目】(本题满分10分)如图,已知AB是⊙O的直径,点C在⊙O上,过点C的直线与AB的延长线交于点P,AC=PC,∠COB=2∠PCB.
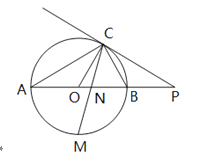
(1)求证:PC是⊙O的切线;
(2)求证:BC=![]() AB;
AB;
(3)点M是弧AB的中点,CM交AB于点N,若AB=4,求MN·MC的值.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=∠90°,D为AB边上一点. 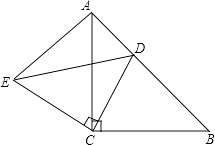
(1)求证:△ACE≌△BCD;
(2)若AD=6,BD=8,求ED的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2). 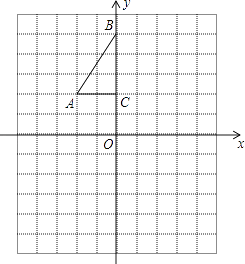
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2 , 请直接写出旋转中心的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B,O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A(3,0),B(0,4),则点B80的坐标为 , 点B81的坐标为 . 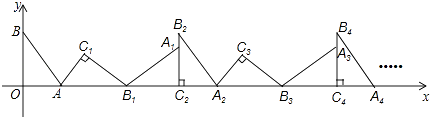
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,O是等边△ABC内一点,OA=6,OB=8,OC=10,以B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:①△BO′A可以由△BOC绕点B逆时针方向旋转60°得到;②连接OO′,则OO′=8;③∠AOB=150°;④ ![]() 其中正确的有( )
其中正确的有( )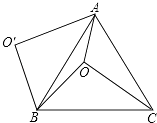
A.①②
B.①②③
C.①②④
D.①②③④
查看答案和解析>>
科目: 来源: 题型:
【题目】甲、乙两种商品原来的单价和为100元,因市场变化,甲商品降价10%,乙商品提价40%,调价后两种商品的单价和比原来的单价和提高了20%、若设甲、乙两种商品原来的单价分别为x元、y元,则下列方程组正确的是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知斜坡AB长为80米,坡角(即∠BAC)为30°,BC⊥AC,现计划在斜坡中点D处挖去部分坡体(用阴影表示)修建一个平行于水平线CA的平台DE和一条新的斜坡BE.
(1)若修建的斜坡BE的坡角为45°,求平台DE的长;(结果保留根号)
(2)一座建筑物GH距离A处36米远(即AG为36米),小明在D处测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G、H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,求建筑物GH的高度.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com