
科目: 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在□ABCD中,AB=2 BC=4,点E、F分别是BC、AD的中点.
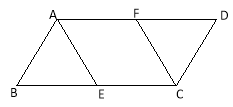
(1)求证:△ABE≌△CDF;
(2)当四边形AECF为菱形时,求出该菱形的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】青藏高原是世界上海拔最高的高原,它的面积约为2500000平方千米.将2500000用科学记数法表示应为( )
A. 25×105 B. 2.5×106 C. 2.5×107 D. 0.25×107
查看答案和解析>>
科目: 来源: 题型:
【题目】已知,△ABC中,AC=BC,∠ACB=90°,D为AB的中点,若E在直线AC上任意一点,DF⊥DE,交直线BC于F点.G为EF的中点,延长CG交AB于点H. 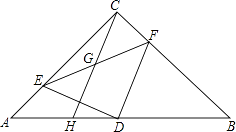
(1)若E在边AC上. ①试说明DE=DF;
②试说明CG=GH;
(2)若AE=3,CH=5.求边AC的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图所示,在Rt△ABC与Rt△OCD中,∠ACB=∠DCO=90°,O为AB的中点.
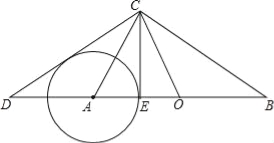
(1)求证:∠B=∠ACD.
(2)已知点E在AB上,且BC2=ABBE.
(i)若tan∠ACD=![]() ,BC=10,求CE的长;
,BC=10,求CE的长;
(ii)试判定CD与以A为圆心、AE为半径的⊙A的位置关系,并请说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,AB=BC,CD⊥AB于点D,CD=BD,BE平分∠ABC,点H是BC边的中点,连接DH,交BE于点G,连接CG. 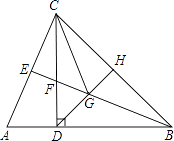
(1)求证:△ADC≌△FDB;
(2)求证:CE= ![]() BF;
BF;
(3)判断△ECG的形状,并证明你的结论;
(4)猜想BG与CE的数量关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com