
科目: 来源: 题型:
【题目】如图1,AB=BC=CD=DA,∠A=∠B=∠BCD=∠ADC=90°,点E是AB上一点,点F是AD延长线上一点,且DF=BE.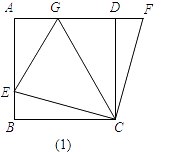
(1)求证:CE=CF;
(2)在图1中,如果点G在AD上,且∠GCE=45°,那么EG=BE+DG是否成立,请说明理由.
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,AD∥BC(BC>AD),∠B=90°,AB=BC=12,点E是AB上一点,且∠DCE=45°,BE=4,求DE的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,所有正方形的中心均在坐标原点,且各边与x轴或y轴平行.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1 , A2 , A3 , A4 , …表示,则顶点A55的坐标是( )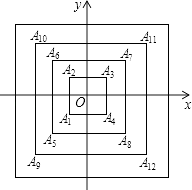
A.(13,13)
B.(﹣13,﹣13)
C.(14,14)
D.(﹣14,﹣14)
查看答案和解析>>
科目: 来源: 题型:
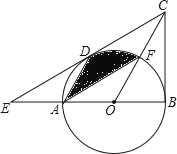
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读下面材料:
小伟遇到这样一个问题:如图1,在△ABC(其中∠BAC是一个可以变化的角)中,AB=2,AC=4,以BC为边在BC的下方作等边△PBC,求AP的最大值.
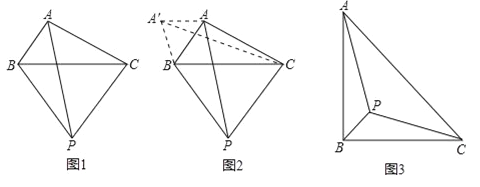
小伟是这样思考的:利用变换和等边三角形将边的位置重新组合.他的方法是以点B为旋转中心将△ABP逆时针旋转60°得到△A′BC,连接A′A,当点A落在A′C上时,此题可解(如图2).
(1)请你回答:AP的最大值是 .
(2)参考小伟同学思考问题的方法,解决下列问题:
如图3,等腰Rt△ABC.边AB=4,P为△ABC内部一点,请写出求AP+BP+CP的最小值长的解题思路.
提示:要解决AP+BP+CP的最小值问题,可仿照题目给出的做法.把△ABP绕B点逆时针旋转60,得到△A′BP′.
①请画出旋转后的图形
②请写出求AP+BP+CP的最小值的解题思路(结果可以不化简).
查看答案和解析>>
科目: 来源: 题型:
【题目】某学生某月有零花钱a元,其支出情况如图所示,那么下列说法不正确的是( ) 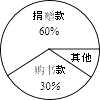
A.该学生捐赠款为0.6a元
B.捐赠款所对应的圆心角为240°
C.捐赠款是购书款的2倍
D.其他消费占10%
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com