
科目: 来源: 题型:
【题目】【阅读材料,获取新知】
善于思考的小军在解方程组![]() 时,采用了一种“整体代换法”的解法.
时,采用了一种“整体代换法”的解法.
解:将方程(2)变形:4x+10y+y=5即2(2x+5y)+y=5(3)
把方程(1)代入(3)得:2×3+y=5
∴y=﹣1.
把y=﹣1,代入(1)得x=4
∴方程组的解为 ![]()
【利用新知,解答问题】
请你利用小军的“整体代换法”解决一下问题:
(1)解方程组:
① ![]() ②
② 
(2)已知x,y满足方程组 ![]() ,则x2+4y2与xy的值分别为、 .
,则x2+4y2与xy的值分别为、 .
查看答案和解析>>
科目: 来源: 题型:
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
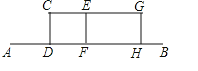
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,∠A=55°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=( ) 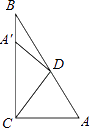
A.40°
B.30°
C.20°
D.10°
查看答案和解析>>
科目: 来源: 题型:
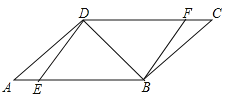
【题目】如图,在ABCD中,点E,F分别在AB,DC上,且ED⊥DB,FB⊥BD.
(1)求证:△AED≌△CFB;
(2)若∠A=30°,∠DEB=45°,求证:DA=DF.
查看答案和解析>>
科目: 来源: 题型:
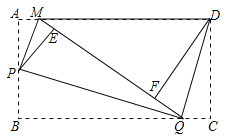
【题目】如图,矩形纸片ABCD,将△AMP和△BPQ分别沿PM和PQ折叠(AP>AM),点A和点B都与点E重合;再将△CQD沿DQ折叠,点C落在线段EQ上点F处.
(1)判断△AMP,△BPQ,△CQD和△FDM中有哪几对相似三角形?(不需说明理由)
(2)如果AM=1,sin∠DMF=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】回答下列问题
(1)问题发现 如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,求∠AEB的度数.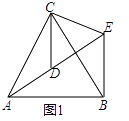
(2)拓展探究 如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请求∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.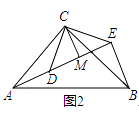
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com