【题目】综合题。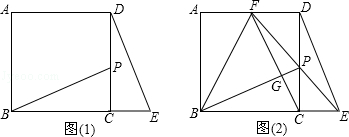

（1）如图（1）点P是正方形ABCD的边CD上一点（点P与点C，D不重合），点E在BC的延长线上，且CE=CP，连接BP，DE．求证：BP=DE且BP⊥DE；
（2）直线EP交AD于F，连接BF，FC．点G是FC与BP的交点．
①若BC=2CE时，求证：BP⊥CF；
②若BC=nCE（n是大于1的实数）时，记△BPF的面积为S1 ， △DPE的面积为S2 ．
求证：S1=（n+1）S2 ．

（1）求每台电脑、每台电子白板各多少万元？

（2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过32万元，但不低于30万元，请你通过计算求出有几种购买方案，哪种方案费用最低．

【题目】如图，已知△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线，交CE的延长线于点F，且AF=BD，连接BF．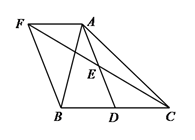

（1）求证：BD=CD；
（2）如果AB=AC，试判断四边形AFBD的形状，并证明你的结论．

（1）求桂味和糯米糍的售价分别是每千克多少元；

（2）如果还需购买两种荔枝共12千克，要求糯米糍的数量不少于桂味数量的2倍，请设计一种购买方案，使所需总费用最低．

（1）设从甲仓库运送到A港口的物资为x吨，求总运费y（元）与x（吨）之间的函数关系式，并写出x的取值范围；

（2）求出最低费用，并说明费用最低时的调配方案．

【题目】下列结论中，正确的是（ ）
A.单项式 的系数是3，次数是2
B.单项式m的次数是1，没有系数
C.单项式-xy2z的系数是一1，次数是4
D.多项式2x2+xy+3是四次三项式

A.在⊙O外B.在⊙O上C.在⊙O内D.不能确定

【题目】如图，四边形ABCD为正方形．点A的坐标为（0，2），点B的坐标为（0，﹣3），反比例函数 的图象经过点C，一次函数y=ax+b的图象经过点A、C，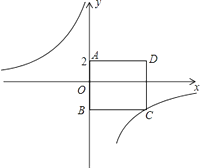

（1）求反比例函数与一次函数的解析式；
（2）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求P点的坐标．