
科目: 来源: 题型:
【题目】某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断: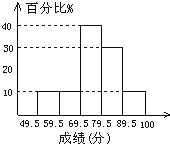
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,E是CD的中点,F是BC上的一点,且∠AEF=90°,延长AE交BC的延长线于点G.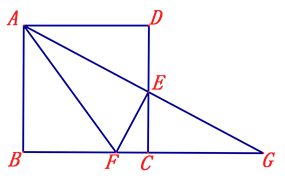
(1)求GE的长;
(2)求证:AE平分∠DAF;
(3)求CF的长.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n , 2).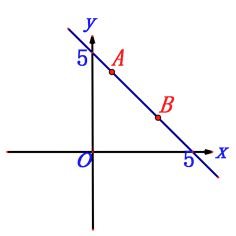
(1)求m、n的值;
(2)当函数图象在第一象限时,自变量x的取值范围是什么?
(3)在x轴上找一点P,使PA+PB最短。求出点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在△ABC中,BD、CE分别是边AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点.
(1)求证:EN与DM互相平分;
(2)若AB=AC,判断四边形DEMN的形状,并说明理由.
查看答案和解析>>
科目: 来源: 题型:
【题目】以下是两张不同类型火车的车票(“Dxxxx次”表示动车,“GXXXX次”表示高铁):
(1)根据车票中的信息填空:该列动车和高铁是向而行(填“相”或“同”).
(2)已知该动车和高铁的平均速度分别为200km/h、300km/h,两列火车的车身长度不计.
①经过测算,如果两列火车直达终点(即中途都不停靠任何站点),高铁比动车将早到1小时,求A、B两地之间的距离(温馨提醒:注意两张火车票的发车时间).
②在①中测算的数据基础上,已知A、B两地途中依次设有5个站点P1、P2、P3、P4、P5 , 且AP1=P1P2=P2P3=P3P4=P4P5=P5B,动车每个站点都停靠,高铁只停靠P2、P4两个站点,两列火车在每个停靠站点都停留5分钟.求该列高铁追上动车的时刻.
查看答案和解析>>
科目: 来源: 题型:
【题目】阅读理解:高斯上小学时,有一次数学老师让同学们计算“从1到100这100个正整数的和”.许多同学都采用了依次累加的计算方法,计算起来非常烦琐,且易出错.聪明的小高斯经过探索后,给出了下面漂亮的解答过程.
解:设S=1+2+3+…+100, ①
则S=100+99+98+…+1,②
①+②,得
2S=101+101+101+…+101.
(两式左右两端分别相加,左端等于2s,右端等于100个101的和)
所以2S=100x101,
S= ![]() ×100X101=5050 ③
×100X101=5050 ③
所以1+2+3+…+100=5050.
后来人们将小高斯的这种解答方法概括为“倒序相加法”.
请解答下面的问题:
(1)请你运用高斯的“倒序相加法”计算:1+2+3+…+200.
(2)请你认真观察上面解答过程中的③式及你运算过程中出现类似的③式,猜想:
1+2+3+…+n= .
(3)计算:101+102+103+…+2018.
查看答案和解析>>
科目: 来源: 题型:
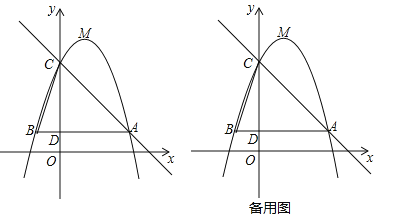
【题目】如图,已知二次函数![]() (b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(b,c为常数)的图象经过点A(3,1),点C(0,4),顶点为点M,过点A作AB∥x轴,交y轴于点D,交该二次函数图象于点B,连结BC.
(1)求该二次函数的解析式及点M的坐标;
(2)若将该二次函数图象向下平移m(m>0)个单位,使平移后得到的二次函数图象的顶点落在△ABC的内部(不包括△ABC的边界),求m的取值范围;
(3)点P是直线AC上的动点,若点P,点C,点M所构成的三角形与△BCD相似,请直接写出所有点P的坐标(直接写出结果,不必写解答过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com