
科目: 来源: 题型:
【题目】某校把学生的笔试成绩、实践能力和成长记录三项成绩分别按50%、20%和30%的比例计入学期总评成绩,90分以上为优秀.甲、乙、丙三人的各项成绩(单位:分)记录如下,学期总评成绩优秀的学生是__________.
笔试成绩 | 实践能力 | 成长记录 | |
甲 | 90 | 83 | 95 |
乙 | 88 | 90 | 95 |
丙 | 90 | 88 | 90 |
查看答案和解析>>
科目: 来源: 题型:
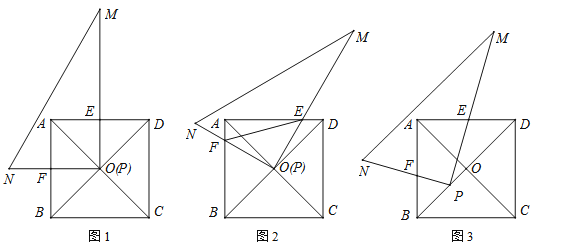
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).

查看答案和解析>>
科目: 来源: 题型:
【题目】在平面直角坐标系中,已知点A(0,0),B(2,﹣2),C(4,0),D(2,2),则以这四个点为顶点的四边形ABCD是( )
A. 正方形 B. 菱形 C. 梯形 D. 矩形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com