
科目: 来源: 题型:
【题目】某市为解决部分市民冬季集中取暖问题需铺设一条长3000米的管道,为尽量减少施工对交通造成的影响,实施施工时“…”,设实际每天铺设管道x米,则可得方程 ![]() ,根据此情景,题中用“…”表示的缺失的条件应补为( )
,根据此情景,题中用“…”表示的缺失的条件应补为( )
A.每天比原计划多铺设10米,结果延期15天才完成
B.每天比原计划少铺设10米,结果延期15天才完成
C.每天比原计划多铺设10米,结果提前15天才完成
D.每天比原计划少铺设10米,结果提前15天才完成
查看答案和解析>>
科目: 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13 200元购进了一批这种衬衫,面市后果然供不应求,商家又用28 800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完利润率不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目: 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图:
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.

查看答案和解析>>
科目: 来源: 题型:
【题目】在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.
(1)求证:AF=DE;
(2)若AC=5,DE=6,则DF= .
(3)试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:
①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)请选择(3)中你探究获得的其中一个结论证明之.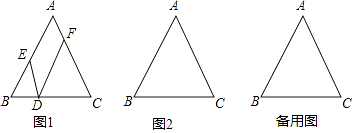
查看答案和解析>>
科目: 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1)按表格数据格式,表中的a=;b=;
(2)请估计:当次数s很大时,摸到白球的频率将会接近;
(3)请推算:摸到红球的概率是(精确到0.1);
(4)试估算:口袋中红球有多少只?
(5)解决了上面4个问题后,请你从统计与概率方面谈一条启示.
查看答案和解析>>
科目: 来源: 题型:
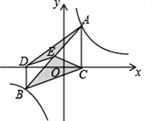
【题目】如图,点A,B在反比例函数![]() (k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
(k>0)的图象上,AC⊥x轴,BD⊥x轴,垂足C,D分别在x轴的正、负半轴上,CD=k,已知AB=2AC,E是AB的中点,且△BCE的面积是△ADE的面积的2倍,则k的值是______.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H. 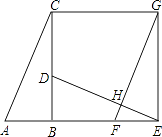
(1)判断线段DE、FG的位置关系,并说明理由;
(2)连结CG,求证:四边形CBEG是正方形.
查看答案和解析>>
科目: 来源: 题型:
【题目】毕达哥拉斯学派对”数”与”形”的巧妙结合作了如下研究:
名称及图形 | 三角形数 | 正方形数 | 五边形数 | 六边形数 |
|
|
|
| |
第一层几何点数 | 1 | 1 | 1 | 1 |
第二层几何点数 | 2 | 3 | 4 | 5 |
第三层几何点数 | 3 | 5 | 7 | 9 |
… | … | … | … | … |
第六层几何点数 | ||||
… | … | … | … | … |
第n层几何点数 |
请写出第六层各个图形的几何点数,并归纳出第n层各个图形的几何点数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com