
科目: 来源: 题型:
【题目】北京等5个城市的国际标准时间(单位:小时)可在数轴上表示如下: ![]()
如果将两地国际标准时间的差简称为时差,那么下列说法中正确的是( )
A. 汉城与纽约的时差为13小时 B. 北京与纽约的时差为13小时
C. 北京与纽约的时差为14小时 D. 北京与多伦多的时差为14小时
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=![]() (k≠0)中k的值的变化情况是( )
(k≠0)中k的值的变化情况是( )
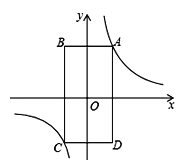
A. 一直增大 B. 一直减小 C. 先增大后减小 D. 先减小后增大
查看答案和解析>>
科目: 来源: 题型:
【题目】如下图。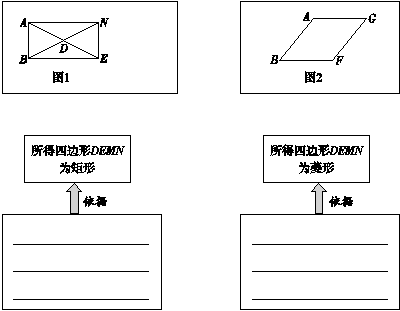
(1)画图-连线-写依据:
先分别完成以下画图(不要求尺规作图),再与判断四边形DEMN形状的相应结论连线,并写出判定依据(只将最后一步判定特殊平行四边形的依据填在横线上).
①如图1,在矩形ABEN中,D为对角线的交点,过点N画直线NP∥DE , 过点E画直线EQ∥DN , NP与EQ的交点为点M , 得到四边形DEMN;
②如图2,在菱形ABFG中,顺次连接四边AB , BF , FG , GA的中点D , E , M , N , 得到四边形DEMN.
(2)请从图1、图2的结论中选择一个进行证明.
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,在一张矩形纸片ABCD中,AD=4cm,点E,F分别是CD和AB的中点.现将这张纸片折叠,使点B落在EF上的点G处,折痕为AH.若HG的延长线恰好经过点D,则CD的长为( )
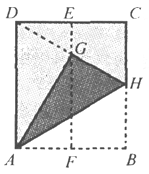
A. 2cm B. ![]() cm C. 4cm D.
cm C. 4cm D. ![]() cm
cm
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,一艘货船以每小时48海里的速度从港口B出发,沿正北方向航行.在港口B处时,测得灯塔A处在B处的北偏西37°方向上,航行至C处,测得A处在C处的北偏西53°方向上,且A、C之间的距离是45海里.在货船航行的过程中,求货船与灯塔A之间的最短距离及B、C之间的距离;若货船从港口B出发2小时后到达D,求A、D之间的距离.
(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
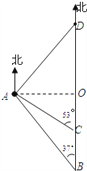
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(2,0),抛物线的对称轴x=-1与抛物线交于点D,与直线BC交于点E.

(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形BOCF的面积最大,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线l与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标.
查看答案和解析>>
科目: 来源: 题型:
【题目】一个不透明的布袋中有4个红球、5个白球、11个黄球,它们除颜色外都相同.
(1)求从袋中摸出一个球是红球的概率;
(2)现从袋中取走若干个黄球,并放入相同数量的红球,搅拌均匀后,要使从袋中摸出一个球是红球的概率不小于![]() ,问至少需取走多少个黄球?
,问至少需取走多少个黄球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com