
科目: 来源: 题型:
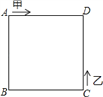
【题目】如图,甲、乙两动点分别从正方形ABCD的顶点A、C同时沿正方形的边开始移动,甲点依顺时针方向环行,乙点依逆时针方向环行.若甲的速度是乙的速度的3倍,则它们第2018次相遇在___边上.
查看答案和解析>>
科目: 来源: 题型:
【题目】某物流公司的快递车和货车同时从甲地出发,以各自的速度匀速向乙地行驶,快递车到达乙地后缷完物品再另装货物共用45分钟,立即按原路以另一速度匀速返回,直至与货车相遇.已知货车的速度为60千米/时,两车之间的距离y(千米)与货车行驶时间x(小时)之间的函数图象如图所示,现有以下4个结论: ①快递车从甲地到乙地的速度为100千米/时;
②甲、乙两地之间的距离为120千米;
③图中点B的坐标为(3 ![]() ,75);
,75);
④快递车从乙地返回时的速度为90千米/时,
以上4个结论正确的是 . 
查看答案和解析>>
科目: 来源: 题型:
【题目】如图1,若△ABC和△ADE为等边三角形,M,N分别EB,CD的中点,易证:CD=BE,△AMN是等边三角形.
(1)当把△ADE绕A点旋转到图2的位置时,CD=BE是否仍然成立?若成立请证明,若不成立请说明理由;
(2)当△ADE绕A点旋转到图3的位置时,△AMN是否还是等边三角形?若是请给出证明,
(3)在(2)的条件下,求出当AB=2AD时,△ADE与△ABC及△AMN的面积之比S△ADE∶S△ABC∶ S△AMN.

查看答案和解析>>
科目: 来源: 题型:
【题目】某商场销售一种西装和领带,西装每套定价200元,领带每条定价40元.国庆节期间商场决定开展促销活动,活动期间向客户提供两种优惠方案:
方案一:买一套西装送一条领带;
方案二:西装和领带都按定价的90%付款.
现某客户要到该商场购买西装20套,领带x![]() .
.
(1)若该客户按方案一购买,需付款多少元(用含x的式子表示)?若该客户按方案二购买,需付款多少元(用含x的式子表示)?
(2)若![]() ,通过计算说明此时按哪种方案购买较为合算;
,通过计算说明此时按哪种方案购买较为合算;
(3)当![]() 时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
时,你能给出一种更为省钱的购买方法吗?试写出你的购买方法和所需费用.
查看答案和解析>>
科目: 来源: 题型:
【题目】平面直角坐标系中,一个三角形的三个顶点的坐标,横坐标保持不变,纵坐标增加3个单位,则所得的图形与原图形相比( ).
A. 形状不变,大小扩大了3倍 B. 形状不变,向右平移了3个单位
C. 形状不变,向上平移了3个单位 D. 三角形被纵向拉伸为原来的3倍
查看答案和解析>>
科目: 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示﹣11,点B表示10,点C表示18,我们称点A和点C在数轴上相距29个长度单位.动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
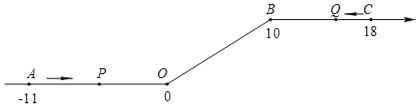
问:(1)动点P从点A运动至C点需要多少时间?
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少;
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目: 来源: 题型:
【题目】第三届世界互联网大会(3rd World Internet Conference),是由中华人民共和国倡导并举办的互联网盛会,于2016年11月16日至18日在浙江乌镇举办.某初中学校为了了解本校学生对本次互联网大会的关注程度(关注程度分为:A.特别关注;B.一般关注;C.偶尔关注;D.不关注),随机抽取了部分学生进行调查,并将结果绘制成频数折线统计图1和扇形统计图2(不完整)请根据图中信息回答问题.
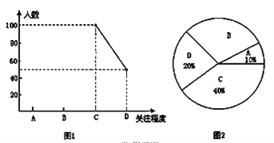
(1)此次抽样调查中,共调查了多少名学生?
(2)求出图2中扇形B所对的圆心角度数,并将图1补充完整.
(3)在这次调查中,九(1)班共有甲、乙、丙、丁四人“特别关注”本届互联网大会,现准备从四人中随机抽取两人进行交流,请用列表法或画树状图的方法求出抽取的两人恰好是甲和乙的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com