练习册

  • 练习册
  • 试题
    相关习题
     0  342723  342731  342737  342741  342747  342749  342753  342759  342761  342767  342773  342777  342779  342783  342789  342791  342797  342801  342803  342807  342809  342813  342815  342817  342818  342819  342821  342822  342823  342825  342827  342831  342833  342837  342839  342843  342849  342851  342857  342861  342863  342867  342873  342879  342881  342887  342891  342893  342899  342903  342909  342917  366461 

    科目： 来源： 题型：

    【题目】下列计算中，正确的是（　　）
    A.2a2+3a2=5a4
    B.（a﹣b）2=a2﹣b2
    C.（a3）3=a6
    D.（﹣2a2）3=﹣8a6

    查看答案和解析>>

    科目： 来源： 题型：

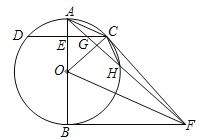
    【题目】如图，已知AB是⊙O的直径，C是⊙O上任一点（不与A，B重合），AB⊥CD于E，BF为⊙O的切线，OF∥AC，连接AF，CF，AF与CD交于点G，与⊙O交于点H，连接CH．

    （1）求证：CF是⊙O的切线；

    （2）求证：EG＝GC；

    （3）若cos∠AOC＝，⊙O的半径为9，求CH的长．

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】已知x＝1是方程x2+ax+2＝0的一个根，则a的值是（　　）

    A.﹣2B.﹣3C.2D.3

    查看答案和解析>>

    科目： 来源： 题型：

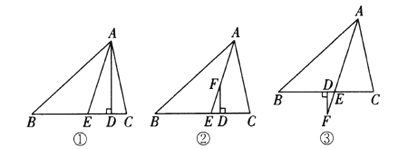
    【题目】在中，.如图①，于点,平分，则易知.

    （1）如图②，平分, 为上的一点，且于点，这时与、有何数量关系?请说明理由;

    （2）如图③，平分,为延长线上的一点，于点，请你写出这时与、之间的数量关系(只写结论，不必说明理由).

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】在△ABC中，BD为∠ABC的平分线．
    （1）如图1，∠C=2∠DBC，∠A=60°，求证：△ABC为等边三角形；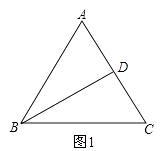

    （2）如图2，若∠A=2∠C，BC=8，AB=4.8，求AD的长度；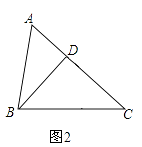

    （3）如图3，若∠ABC=2∠ACB，∠ACB的平分线OC与BD相交于点O，且OC=AB，求∠A的度数．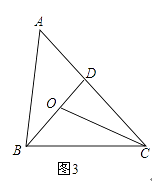

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】商店购进一种商品进行销售，进价为每件40元，售价为每件60元，每月可卖出300件．市场调查反映：调整价格时，售价每涨1元每月要少卖10件；售价每下降1元每月要多卖20件．为了获得更大的利润，现将商品售价调整为60＋x（元/件）（x＞0即售价上涨，x＜0即售价下降），每月商品销量为y（件），月利润为w（元）．

    （1）直接写出y与x之间的函数关系式；

    （2）当销售价格是多少时才能使月利润最大？最大月利润时多少？

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】计算：（3m）33n=（　　）
    A.3mn
    B.33m+n
    C.27mn
    D.27m+n

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】把抛物线y=3x2向右平移一个单位,则所得抛物线的解析式为( )

    A.y=3(x+1)2B.y=3(x-1)2C.y=3x2+1D.y=3x2-1

    查看答案和解析>>

    科目： 来源： 题型：

    【题目】如图，在△ABC中(BC>AC)，∠ACB=90°，点D在AB边上，DE⊥AC于点E.设点F在线段EC上，点G在射线CB上，以F，C，G为顶点的三角形与△EDC有一个锐角相等，FG交CD于点P，问：线段CP可能是△CFG的高线还是中线？或两者都有可能？请说明理由.

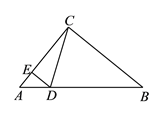
    查看答案和解析>>

    科目： 来源： 题型：

    【题目】阅读下面的材料:

    如图①，在中，试说明.

    分析:通过画平行线，将、、作等量代换，使各角之和恰为一个平角，依辅助线不同而得多种方法.

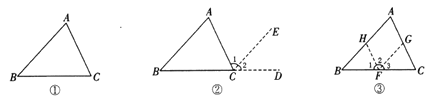
    解:如图②，延长到点,过点作 //.

    因为//(作图所知)，

    所以,(两直线平行，同位角、内错角相等).

    又因为(平角的定义)，

    所以(等量代换).

    如图③，过上任一点，作//, //，这种添加辅助线的方法能说吗?并说明理由.

    查看答案和解析>>

    同步练习册答案