(1)求线段MN的长．

(2)若C为线段AB上任一点，满足AC＋CB＝a cm，其他条件不变，你能猜想MN的长度吗？（用含a的代数式表示）并说明理由．

A.y1>y2B.y1＝y2C.y1<y2D.不能确定

（1）小红同学参加了竞赛，成绩是90分，请问小红在竞赛中答对了多少道题？

（2）小明也参加了竞赛，考完后他说：“这次竞赛我一定能拿到100分．”请问小明有没有可能拿到100分？试用方程的知识来说明理由．

【题目】若三角形的两边长分别为6cm，9cm，则其第三边的长可能为（ ）
A.2cm
B.3cm
C.7cm
D.16cm

【题目】如图，已知线段AB和CD的公共部分BD=AB= CD，线段AB、CD的中点E，F之间距离是10cm，求AB，CD的长．

（1）若设每件降价x（x为整数）元，每星期售出商品的利润为y元，请写出x与y之间的函数关系式，并求出自变量x的取值范围；

（2）请画出上述函数的大致图象.

（3）当降价多少元时，每星期的利润最大？最大利润是多少？

小丽解答过程如下：

解：（1）根据题意，可列出表达式：

y=(60-x)(300+20x)-40(300+20x),

即y=-20x2+100x+6000.

∵降价要确保盈利，∴40＜60-x60.解得0x＜20.

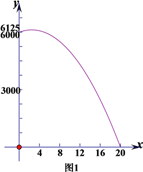
（2）上述表达式的图象是抛物线的一部分，函数的大致图象如图1：

（3）∵a=-20＜0，

∴当x==2.5时，y有最大值，y==6125.

所以，当降价2.5元时，每星期的利润 最大，最大利润为6125.

老师看了小丽的解题过程，说小马第（1）问的表达式是正确的，但自变量x的取值范围不准确.（2）（3）问的答案，也都存在问题.请你就老师说的问题，进行探究，写出你认为（1）（2）（3）中正确的答案，或说明错误原因.

A. 测量对角线是否平分 B. 测量两组对边是否分别相等

C. 测量其中三个角是否是直角 D. 测量对角线是否相等

【题目】水龙头关闭不严会造成滴水，为了调查漏水量与漏水时间的关系，可在滴水的水龙下放置一个水杯，每5分钟称一次水杯的重，如下表：

若水杯的重量w是滴水时间t的一次函数，则滴水时间为32分时，水杯的重量为（ ）
A.107克
B.110克
C.113克
D.116克

【题目】下列运算正确的是（ ）
A.xx2=x2
B.（xy）2=xy2
C.（x2）3=x6
D.x2+x2=x4